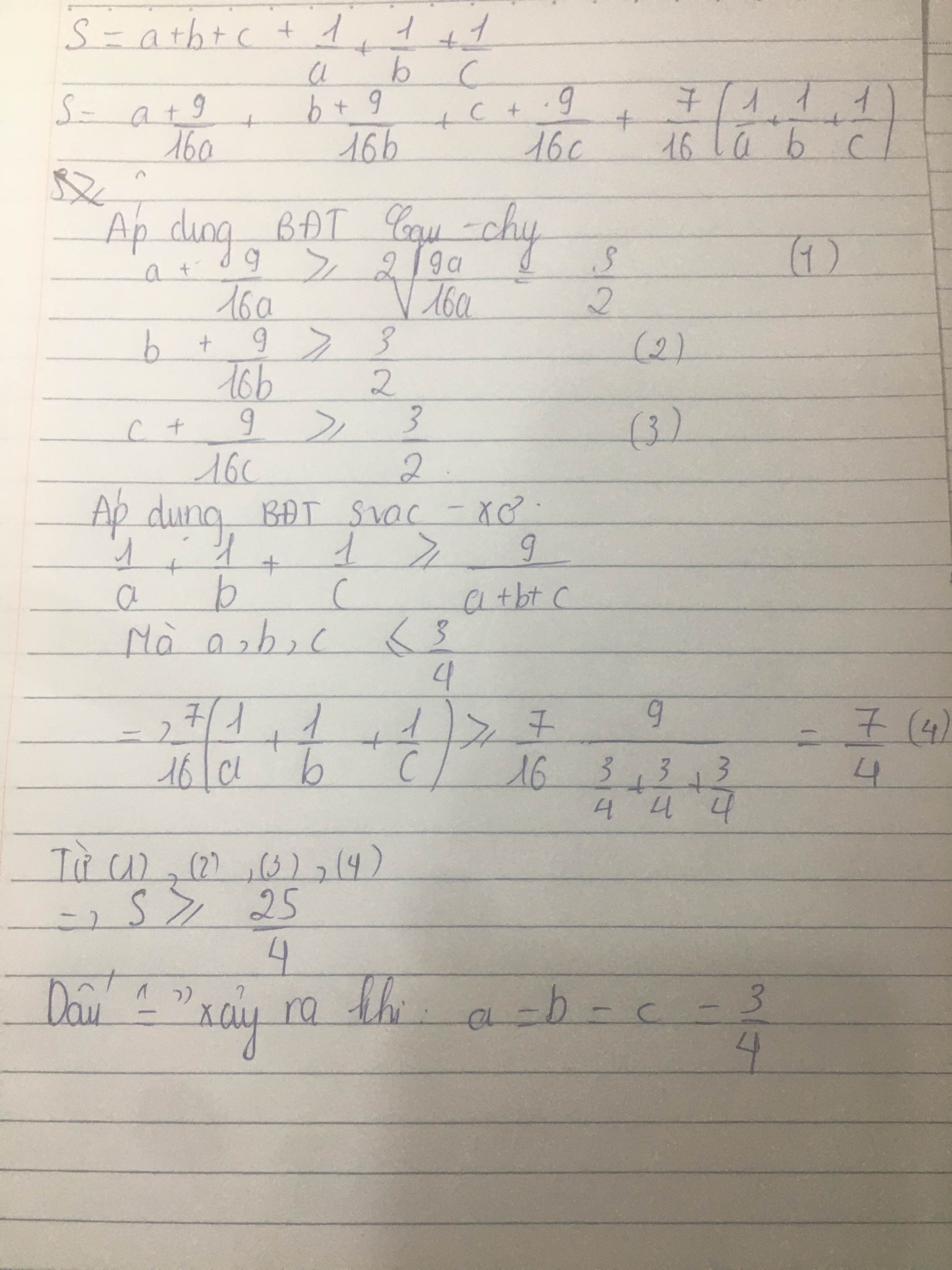Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{4c}{4c+57}\ge\frac{1}{1+a}+\frac{35}{35+2b}\ge2\sqrt{\frac{35}{\left(1+a\right)\left(35+2b\right)}}\)
\(\frac{a}{1+a}\ge\frac{57}{4c+57}+\frac{35}{35+2b}\ge2\sqrt{\frac{35\cdot57}{\left(4c+57\right)\left(35+2b\right)}}\)
\(\frac{2b}{35+2b}\ge\frac{57}{4c+57}+\frac{1}{1+a}\ge2\sqrt{\frac{57}{\left(4c+57\right)\left(1+a\right)}}\)
\(\Rightarrow8abc\ge8\cdot1995\Rightarrow abc\ge1995\)
Vậy giá trị nhỏ nhất của abc là 1995

\(P=\dfrac{4ab}{a+2b}+\dfrac{9ca}{a+4c}+\dfrac{4bc}{b+c}\)
\(P=\dfrac{4abc}{ac+2bc}+\dfrac{9abc}{ab+4bc}+\dfrac{4abc}{ab+ac}\)
\(P=abc\left(\dfrac{4}{ac+2bc}+\dfrac{9}{ab+4bc}+\dfrac{4}{ab+ac}\right)\)
\(P\ge abc.\dfrac{\left(2+3+2\right)^2}{ac+2bc+ab+4bc+ab+ac}\)
\(P\ge abc.\dfrac{49}{2ab+6bc+2ca}\)
\(P\ge abc.\dfrac{49}{7abc}\) (vì \(2ab+6bc+2ca=7abc\))
\(P\ge7\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{ac+2bc}=\dfrac{3}{ab+4bc}=\dfrac{2}{ab+ac}\\2ab+6bc+2ca=7abc\end{matrix}\right.\)
\(\dfrac{2}{ac+2bc}=\dfrac{2}{ab+ac}\) \(\Leftrightarrow2b=a\)
Có \(\dfrac{3}{ab+4bc}=\dfrac{2}{ab+ac}\)
\(\Leftrightarrow\dfrac{3}{2b^2+4bc}=\dfrac{2}{2b^2+2bc}\)
\(\Leftrightarrow3b^2+3bc=2b^2+4bc\)
\(\Leftrightarrow b^2=bc\Leftrightarrow b=c\)
\(\Rightarrow a=2b=2c\)
Lại có \(2ab+6bc+2ca=7abc\) \(\Rightarrow4b^2+6b^2+4b^2=14b^3\)
\(\Leftrightarrow b=1\)
\(\Leftrightarrow\left(a,b,c\right)=\left(2,1,1\right)\)
Vậy \(min_P=7\)

\(2ab+6bc+2ac=7abc\Rightarrow\dfrac{6}{a}+\dfrac{2}{b}+\dfrac{2}{c}=7\)
Đặt \(\left(\dfrac{2}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow3x+2y+2z=7\)
\(C=\dfrac{4}{\dfrac{2}{a}+\dfrac{1}{b}}+\dfrac{9}{\dfrac{4}{a}+\dfrac{1}{c}}+\dfrac{4}{\dfrac{1}{b}+\dfrac{1}{c}}=\dfrac{4}{x+y}+\dfrac{9}{2x+z}+\dfrac{4}{y+z}\)
\(C\ge\dfrac{\left(2+3+2\right)^2}{x+y+2x+z+y+z}=\dfrac{49}{7}=7\)
Dấu "=" xảy ra khi \(x=y=z=1\) hay \(\left(a;b;c\right)=\left(2;1;1\right)\)

\(P=\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ac}+\dfrac{1}{a^2+b^2+c^2}\ge\dfrac{\left(1+1+1\right)^2}{ab+bc+ca}+\dfrac{1}{a^2+b^2+c^2}\) (BĐT Cauchy Schwarz)
\(=\dfrac{9}{ab+bc+ca}+\dfrac{1}{a^2+b^2+c^2}\)
\(=\dfrac{1}{ab+bc+ca}+\dfrac{1}{ab+bc+ca}+\dfrac{1}{a^2+b^2+c^2}+\dfrac{7}{ab+bc+ca}\)
\(\ge\dfrac{\left(1+1+1\right)^2}{a^2+b^2+c^2+2ab+2ac+2bc}+\dfrac{7}{ab+bc+ca}\)
\(=\dfrac{9}{\left(a+b+c\right)^2}+\dfrac{7}{ab+bc+ca}\)
Ta có: \(ab+bc+ca\le\dfrac{\left(a+b+c\right)^2}{3}=\dfrac{1}{3}\) .Thế vào biểu thức
\(\Rightarrow P\ge9+\dfrac{7}{\dfrac{1}{3}}=9+21=30\)
\(\Rightarrow P_{min}=30\) khi \(a=b=c=\dfrac{1}{3}\)

Áp dụng bất đẳng thức: \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\) \(\Leftrightarrow a^2+2ab+b^2\ge4ab\Leftrightarrow a^2-2ab+b^2\ge0\Leftrightarrow\left(a-b\right)^2\ge0\left(đúng\right)\)
\(\dfrac{1}{2a+b+c}=\dfrac{1}{4}.\dfrac{4}{2a+b+c}\le\dfrac{1}{4}\left(\dfrac{1}{2a}+\dfrac{1}{b+c}\right)\le\dfrac{1}{4}\left[\dfrac{1}{2a}+\dfrac{1}{4}\left(\dfrac{1}{b}+\dfrac{1}{c}\right)\right]=\dfrac{1}{8}\left(\dfrac{1}{a}+\dfrac{1}{2b}+\dfrac{1}{2c}\right)\)
CMTT \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{a+2b+c}\le\dfrac{1}{8}\left(\dfrac{1}{2a}+\dfrac{1}{b}+\dfrac{1}{2c}\right)\\\dfrac{1}{a+b+2c}\le\dfrac{1}{8}\left(\dfrac{1}{2a}+\dfrac{1}{2b}+\dfrac{1}{c}\right)\end{matrix}\right.\)
\(\Rightarrow M=\dfrac{1}{2a+b+c}+\dfrac{1}{a+2b+c}+\dfrac{1}{a+b+2c}\le\dfrac{1}{8}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{2}{2a}+\dfrac{2}{2b}+\dfrac{2}{2c}\right)=\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{1}{4}.4=1\)
\(minM=1\Leftrightarrow a=b=c=\dfrac{3}{4}\)

\(\Leftrightarrow\frac{1}{1+a}+\frac{a}{1+a}+\frac{2b}{21+2b}+\frac{21}{21+2b}\le\frac{4c}{4c+27}+\frac{a}{1+a}+\frac{2b}{21+2b}\)
\(\Leftrightarrow2\le\frac{1}{1+\frac{1}{a}}+\frac{1}{1+\frac{21}{2b}}+\frac{1}{1+\frac{27}{4c}}\)
Đặt \(\left(\frac{1}{a};\frac{21}{2b};\frac{27}{4c}\right)=\left(x;y;z\right)\)
\(\Leftrightarrow\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\ge2\)
\(\Leftrightarrow\frac{1}{1+x}\ge1-\frac{1}{1+y}+1-\frac{1}{1+z}=\frac{y}{1+y}+\frac{z}{1+z}\ge2\sqrt{\frac{yz}{\left(1+y\right)\left(1+z\right)}}\)
Tương tự: \(\frac{1}{1+y}\ge2\sqrt{\frac{zx}{\left(1+z\right)\left(1+x\right)}}\) ; \(\frac{1}{1+z}\ge2\sqrt{\frac{xy}{\left(1+x\right)\left(1+y\right)}}\)
Nhân vế với vế: \(1\ge8xyz\Rightarrow xyz\le\frac{1}{8}\)
\(\Leftrightarrow\frac{1}{a}.\frac{21}{2b}.\frac{27}{4c}\le\frac{1}{8}\Leftrightarrow abc\ge567\)
Dấu "=" xảy ra khi \(\frac{1}{a}=\frac{21}{2b}=\frac{27}{4c}=\frac{1}{2}\Rightarrow\left(a;b;c\right)=\left(2;21;\frac{27}{2}\right)\)