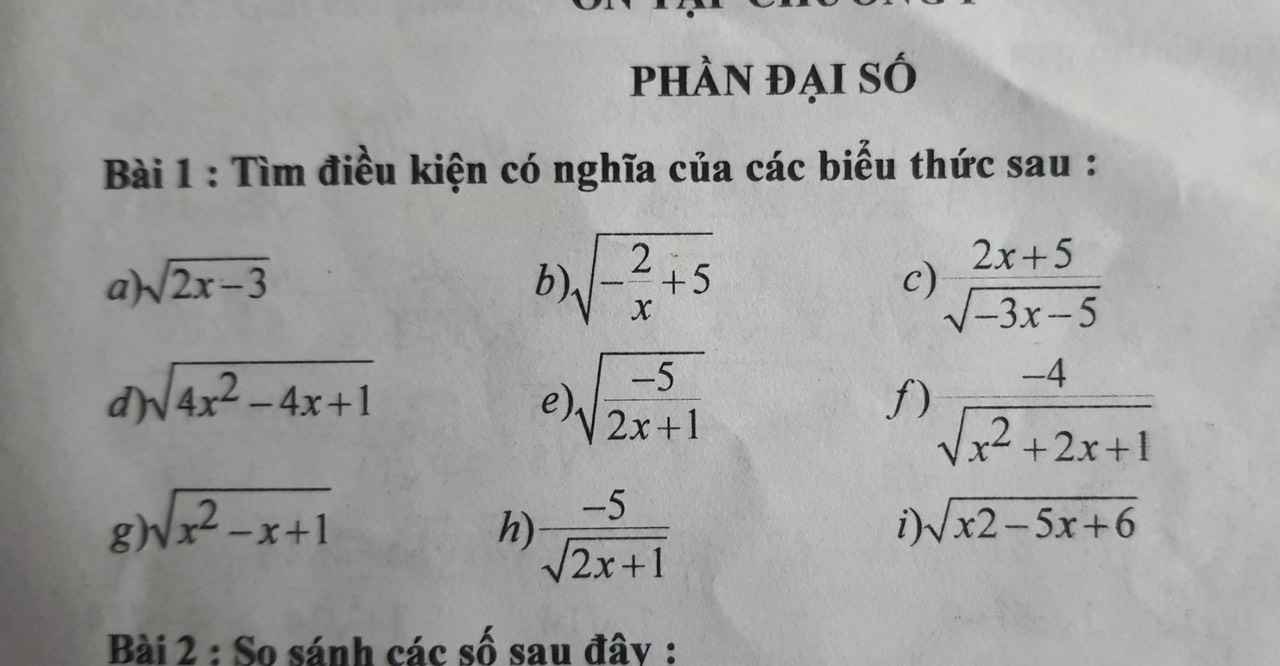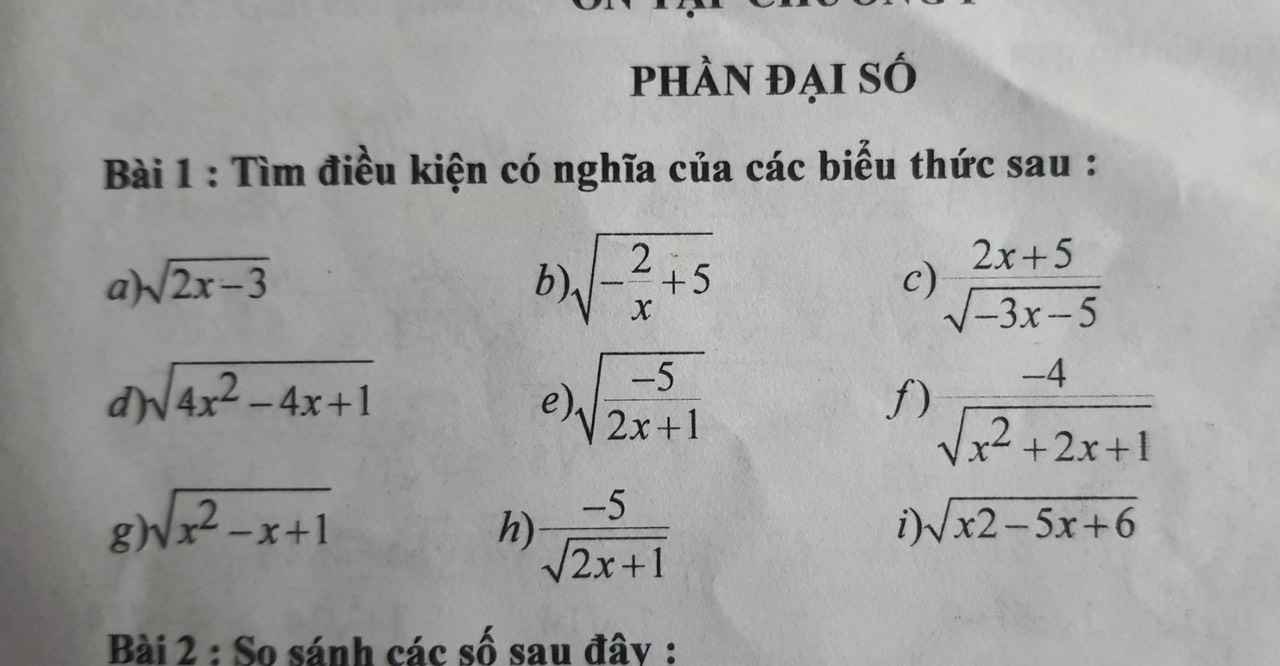Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét ΔMNP vuông tại M có MH là đường cao
nên \(NH\cdot NP=MN^2\left(1\right)\)
Xét ΔMNK vuông tại M có MQ là đường cao
nên \(NQ\cdot NK=MN^2\left(2\right)\)
Từ (1) và (2) suy ra \(NH\cdot NP=NQ\cdot NK\)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM\(\perp\)MB tại M
=>AM\(\perp\)SB tại M
Xét tứ giác SPAM có \(\widehat{SPA}+\widehat{SMA}=180^0\)
nên SPAM là tứ giác nội tiếp
=>S,P,A,M cùng thuộc một đường tròn
b: Cái này mình xin nói luôn về góc nội tiếp nha bạn: Góc nội tiếp là góc có đỉnh thuộc vào đường tròn, có hai cạnh là hai dây của đường tròn.
Tính chất thì sẽ là Góc nội tiếp bằng một nửa số đo cung bị chắn
Bây giờ mình xin phép làm như sau nha:
M đối xứng M' qua AB
=>AB là đường trung trực của MM'
=>AB\(\perp\)MM' tại trung điểm của MM' và AM=AM'
AM=AM'
=>ΔAMM' cân tại A
AB\(\perp\)MM'
SS'\(\perp\)BA
Do đó: MM'//SS'
Xét ΔAMM' và ΔAS'S có
\(\widehat{AMM'}=\widehat{AS'S}\)(hai góc so le trong, MM'//SS')
\(\widehat{MAM'}=\widehat{S'AS}\)(hai góc đối đỉnh)
Do đó: ΔAMM'\(\sim\)ΔAS'S
=>\(\dfrac{AM}{AS'}=\dfrac{AM'}{AS}\)
mà AM=AM'
nên AS'=AS
=>ΔAS'S cân tại A
=>\(\widehat{ASS'}=\widehat{AS'S}\)
mà \(\widehat{ASS'}=\widehat{AMP}\)(APSM là tứ giác nội tiếp)
nên \(\widehat{PS'M}=\widehat{PMS'}\)
=>ΔPS'M cân tại P

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

\(P=\dfrac{2\sqrt{x}}{\sqrt{x}+3}\left(x\ge0\right)\)
để P>\(\dfrac{1}{4}< =>\dfrac{2\sqrt{x}}{\sqrt{x}+3}>\dfrac{1}{4} < =>\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{1}{4}>0\)
<=>\(\dfrac{4.2\sqrt{x}}{4\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}+3}{4\left(\sqrt{x}+3\right)}>0\)
<=>\(\dfrac{8\sqrt{x}-\sqrt{x}-3}{4\left(\sqrt{x}+3\right)}>0< =>\dfrac{7\sqrt{x}-3}{4\left(\sqrt{x}+3\right)}>0\)
ta có \(\sqrt{x}\ge0\left(\forall x\right)=>\sqrt{x}+3\ge3=>4\left(\sqrt{x}+3\right)>12\)
hay \(4\left(\sqrt{x}+3\right)>0\)
vậy để \(\dfrac{7\sqrt{x}-3}{4\left(\sqrt{x}+3\right)}>0< =>7\sqrt{x}-3>0< =>7\sqrt{x}>3< =>\sqrt{x}>\dfrac{3}{7}\)
<=>\(x>\dfrac{9}{49}\)
vậy x>9/49 thì pP>1/4

a: ĐKXĐ: \(x\ge\dfrac{3}{2}\)
c: ĐKXĐ: \(x< -\dfrac{5}{3}\)
d: ĐKXĐ: \(x\in R\)
e: ĐKXĐ: \(x< -\dfrac{1}{2}\)
f: ĐKXĐ: \(x\ne-1\)
g: ĐKXĐ: \(x\in R\)
h: ĐKXĐ: \(x>-\dfrac{1}{2}\)
b: ĐKXĐ: \(\left\{{}\begin{matrix}x\le\dfrac{2}{5}\\x\ne0\end{matrix}\right.\)

a) ĐKXĐ: \(2x-3\ge0\Rightarrow x\ge\dfrac{3}{2}\)
b) ĐKXĐ: \(-\dfrac{2}{x}+5\ge0\Rightarrow x\ge\dfrac{2}{5}\)
c)ĐKXĐ: \(-3x-5>0\Rightarrow x>-\dfrac{5}{3}\)
d) ĐKXĐ: \(4x^2-4x+1\ge0\Rightarrow\left(2x-1\right)^2\ge0\) (luôn đúng)


Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

9:
\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-2m+4\right)\)
=4m^2-4m^2+8m-16=8m-16
Để phương trình có hai nghiệm phân biệt thì 8m-16>0
=>m>2
x1^2+x2^2=x1+x2+8
=>(x1+x2)^2-2x1x2-(x1+x2)=8
=>(2m)^2-2(m^2-2m+4)-2m=8
=>4m^2-2m^2+4m-8-2m=8
=>2m^2+2m-16=0
=>m^2+m-8=0
mà m>2
nên \(m=\dfrac{-1+\sqrt{33}}{2}\)