K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
YH
0
YH
0
3T
1
18 tháng 6 2023
4:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hcn
=>ΔACD vuông tại C
b: Xét ΔKAB vuông tại A và ΔKCD vuông tại C có
KA=KC
AB=CD
=>ΔKAB=ΔKCD
=>KB=KD
c: Xét ΔACD có
DK,CM là trung tuyến
DK cắt CM tại I
=>I là trọng tâm
=>KI=1/3KD
Xét ΔCAB có
AM,BK là trung tuyến
AM cắt BK tại N
=>N là trọng tâm
=>KN=1/3KB=KI
TN
0
17 tháng 4 2021
a, Ta có : \(P\left(x\right)+Q\left(x\right)=x^2-4x+3+3x^2-4x+1=4x^2-8x+4\)
\(P\left(x\right)-Q\left(x\right)=x^2-4x+3-3x^2+4x-1=-2x^2+2\)
17 tháng 4 2021
b, Vì x = 1 là nghiệm của P(x) + Q(x) nên
Thay x = 1 vào P(x) + Q(x) ta được
\(4-8+4=0\)* đúng *
NA
19 tháng 5 2021
a, M(x)= 3x^3 - 2x^2 + 1 (đã rút gọn ) , ý b bạn chỉ cần thay M(-1) và M(2) vào x lần lượt từng con là đc vd : M(-1)= 3* (-1^3) - 2* (- 1)^2 + 1 rồi tính ra kết quả là được
2H
1
OY
28 tháng 9 2021
a) Vì \(\left|2x+4\right|\ge0;\left|y\right|\ge0\)
mà \(\left|2x+4\right|+\left|y\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|2x+4\right|=0\\\left|y\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(-2;0\right)\)
NT
5
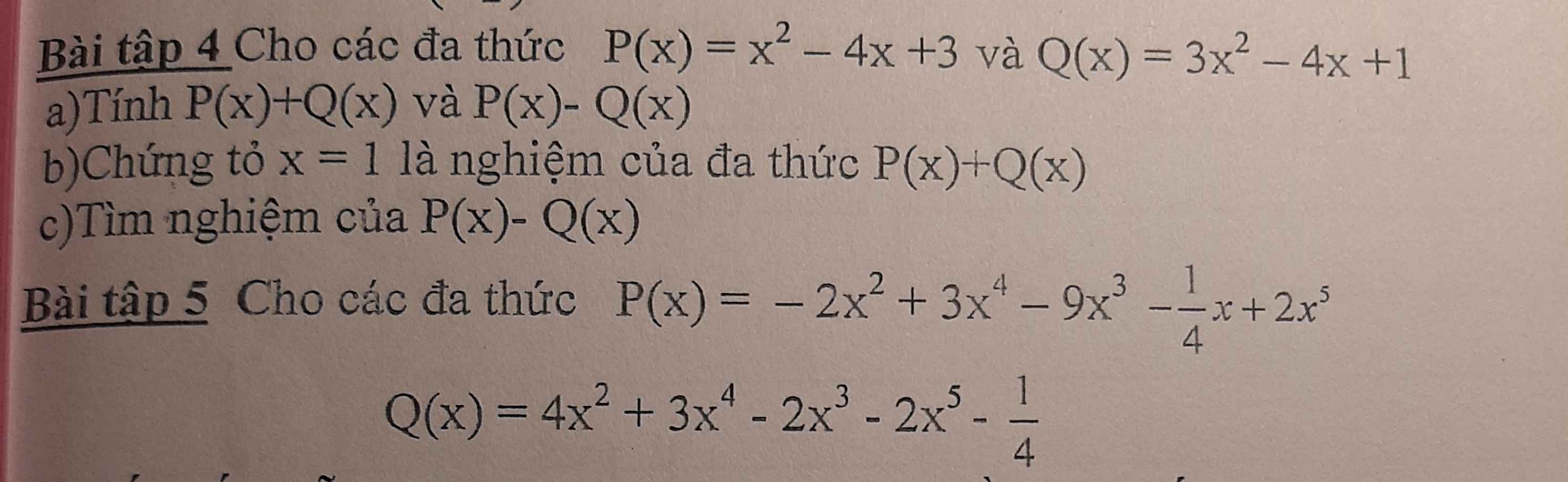
a, Xét tam giác ABC cân tại A
có AH là đường cao
đồng thời là đường phân giác, đường trung tuyến
=> HB = HC ; ^BAH = ^CAH
b, Ta có HB = BC/2 = 4 cm
Xét tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-HB^2}=3cm\)
c, Xét tam giác ADH và tam giác AEH
AH _ chung
^DAH = ^EAH (cmt)
Vậy tam giác ADH = tam giác AEH (ch-cgv)
=> DH = EH ( 2 cạnh tương ứng )
Vậy tam giác HDE cân tại H