
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

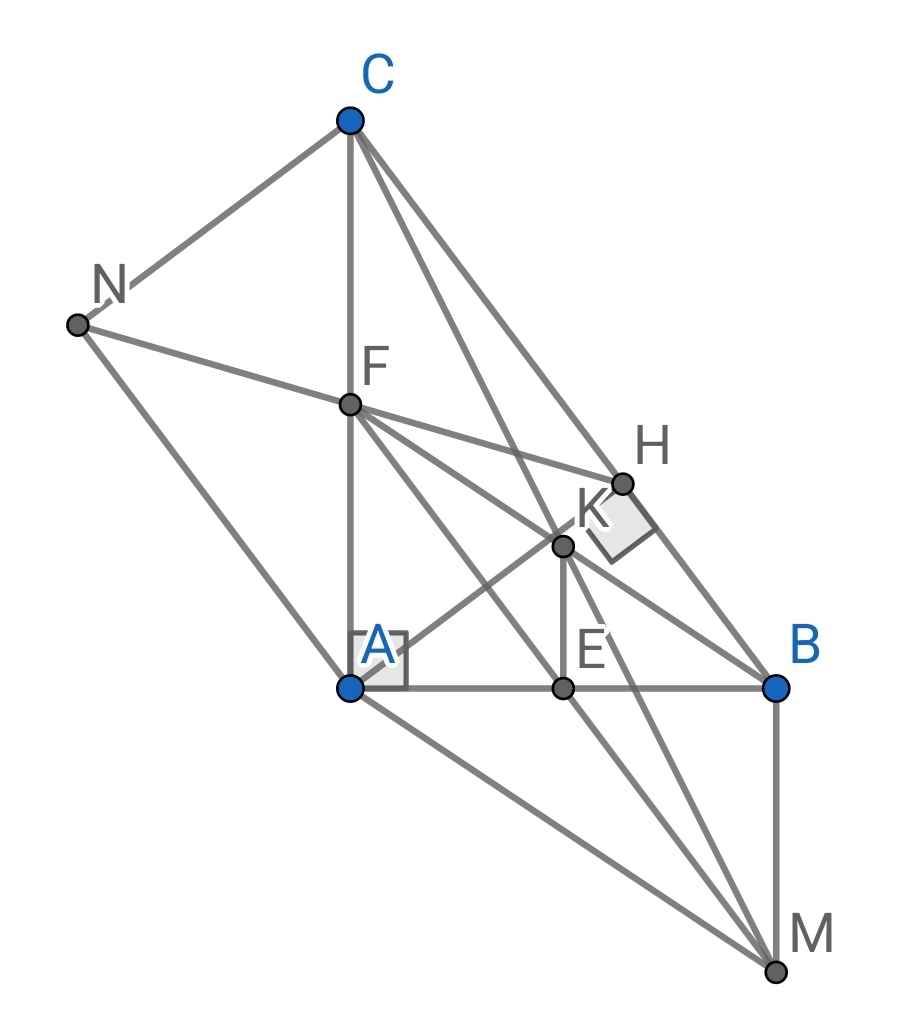 c) Do AMBF là hình bình hành (cmt)
c) Do AMBF là hình bình hành (cmt)
⇒ BM // AF
Mà AF ⊥ AB
⇒ BM ⊥ AB
⇒ ∠ABM = 90⁰
Do AHCN là hình chữ nhật (cmt)
⇒ ∆AHC vuông tại H
F là trung điểm của AC (gt)
⇒ HF = AF = CF = AC : 2
⇒ ∆AHF cân tại F
⇒ ∠AHF = ∠FAH
Mà ∠FAH + ∠HAB = 90⁰
⇒ ∠AHF + ∠HAB = 90⁰
Lại có:
∆AHB vuông tại H
⇒ ∠HAB + ∠HBA = 90⁰
Mà ∠HAB + ∠AHF = 90⁰ (cmt)
⇒ ∠AHF = ∠HBA (1)
Do ∠FHB = ∠AHF + ∠AHB
= ∠AHF + 90⁰ (2)
∠MBH = ∠HBA + ∠ABM
= HBA + 90⁰ (3)
Từ (1), (2), (3) ⇒ ∠FHB = ∠MBH
∆ABC có:
E là trung điểm của AB (gt)
F là trung điểm của AC (gt)
⇒ EF // BC
⇒ FM // BH
Tứ giác BMFH có:
FM // BH (cmt)
⇒ BMFH là hình thang
Mà ∠FHB = ∠MBH (cmt)
⇒ BMFH là hình thang cân
d)
Do AMBF là hình bình hành (cmt)
⇒ AF = BM và AF // BM
Do F là trung điểm của AC (gt)
⇒ AF = CF = AC : 2
⇒ AC = 2AF
Mà AF = BM (cmt)
⇒ CF = BM
Do AF // BM (cmt)
⇒ CF // BM
Tứ giác BCFM có:
CF // BM (cmt)
CF = BM (cmt)
⇒ BCFM là hình bình hành
Mà K là giao điểm của BF và CM (gt)
⇒ K là trung điểm của BF
∆FBM có:
K là trung điểm của BF (cmt)
E là trung điểm của FM (gt)
⇒ EK là đường trung bình của BM
⇒ EK = BM : 2
⇒ BM = 2EK
Do AHCN là hình chữ nhật (cmt)
⇒ AC = HN
Lại có AC = 2AF (cmt)
⇒ HN = 2AF
Mà AF = BM
⇒ HN = 2BM
Mà BM = 2EK
⇒ HN = 2.2EK = 4EK
Vậy HN = 4EK

Bạn nên viết lại đề cho rõ ràng để nhận được sự trợ giúp tốt hơn nhé.


a: \(A=\dfrac{x\left(x+2\right)}{\left(x-2\right)^2}:\dfrac{x^2-4+x+6-x^2}{x\left(x-2\right)}\)
\(=\dfrac{x\left(x+2\right)}{x-2}\cdot\dfrac{x}{x+2}=\dfrac{x^2}{x-2}\)
c: A<0
=>x-2<0
=>x<2
d: B nguyên
=>x^2-4+4 chia hết cho x-2
=>x-2 thuộc {1;-1;2;-2;4;-4}
=>x thuộc {3;1;4;6}

Bài 4:
c) Ta có: \(\dfrac{x^3}{8}+\dfrac{x^2y}{2}+\dfrac{xy^2}{6}+\dfrac{y^3}{27}\)
\(=\left(\dfrac{x}{2}\right)^3+3\cdot\left(\dfrac{x}{2}\right)^2\cdot\dfrac{y}{3}+3\cdot\dfrac{x}{2}\cdot\left(\dfrac{y}{3}\right)^2+\left(\dfrac{y}{3}\right)^3\)
\(=\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^3\)
\(=\left(\dfrac{-1}{2}\cdot8+\dfrac{1}{3}\cdot6\right)^3=\left(-4+2\right)^3=-8\)

c: Gọi bốn số nguyên liên tiếp là x;x+1;x+2;x+3
Ta có: \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+3x\right)\left(x^2+3x+2\right)+1\)
\(=\left(x^2+3x\right)^2+2\left(x^2+3x\right)+1\)
\(=\left(x^2+3x+1\right)^2\)
\(d,M=\left(x^2-4xy+4y^2\right)-2\left(x-2y\right)+1+9\\ M=\left(x-2y\right)^2-2\left(x-2y\right)+1+9\\ M=\left(x-2y+1\right)^2+9\ge9\\ M_{min}=9\Leftrightarrow x=2y-1\)


c: ĐKXĐ: x<>8
\(\dfrac{3}{2x-16}+\dfrac{3x-20}{x-8}+\dfrac{1}{8}=\dfrac{13x-102}{3x-24}\)
=>\(\dfrac{9}{6\left(x-8\right)}+\dfrac{18x-120}{6\left(x-8\right)}-\dfrac{26x-204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{18x-111-26x+204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{-8x+93}{6x-48}=\dfrac{-1}{8}\)
=>\(\dfrac{8x-93}{6x-48}=\dfrac{1}{8}\)
=>8(8x-93)=6x-48
=>64x-744-6x+48=0
=>58x=696
=>x=12
d: ĐKXĐ: x<>1; x<>-1
\(\dfrac{6}{x^2-1}+5=\dfrac{8x-1}{4x+4}+\dfrac{12x-1}{4x-4}\)
=>\(\dfrac{24}{4\left(x-1\right)\left(x+1\right)}+\dfrac{20\left(x^2-1\right)}{4\left(x-1\right)\left(x+1\right)}=\dfrac{\left(8x-1\right)\left(x-1\right)+\left(12x-1\right)\left(x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)
=>8x^2-9x+1+12x^2+12x-x-1=24+20x^2-20
=>20x^2+2x=20x^2+4
=>2x=4
=>x=2(loại)

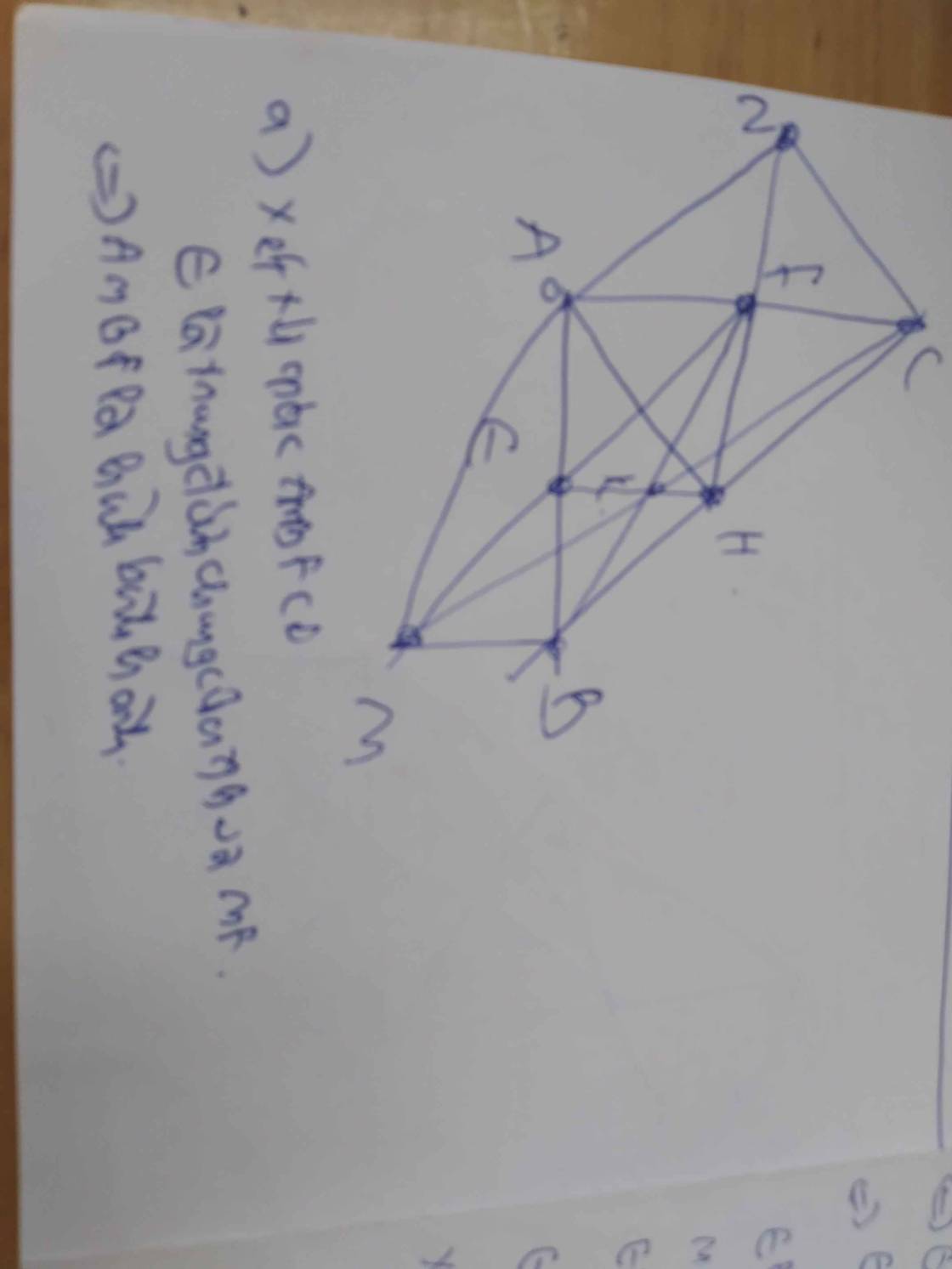







 giúp mình bài 4 câu B,C D với ạ
giúp mình bài 4 câu B,C D với ạ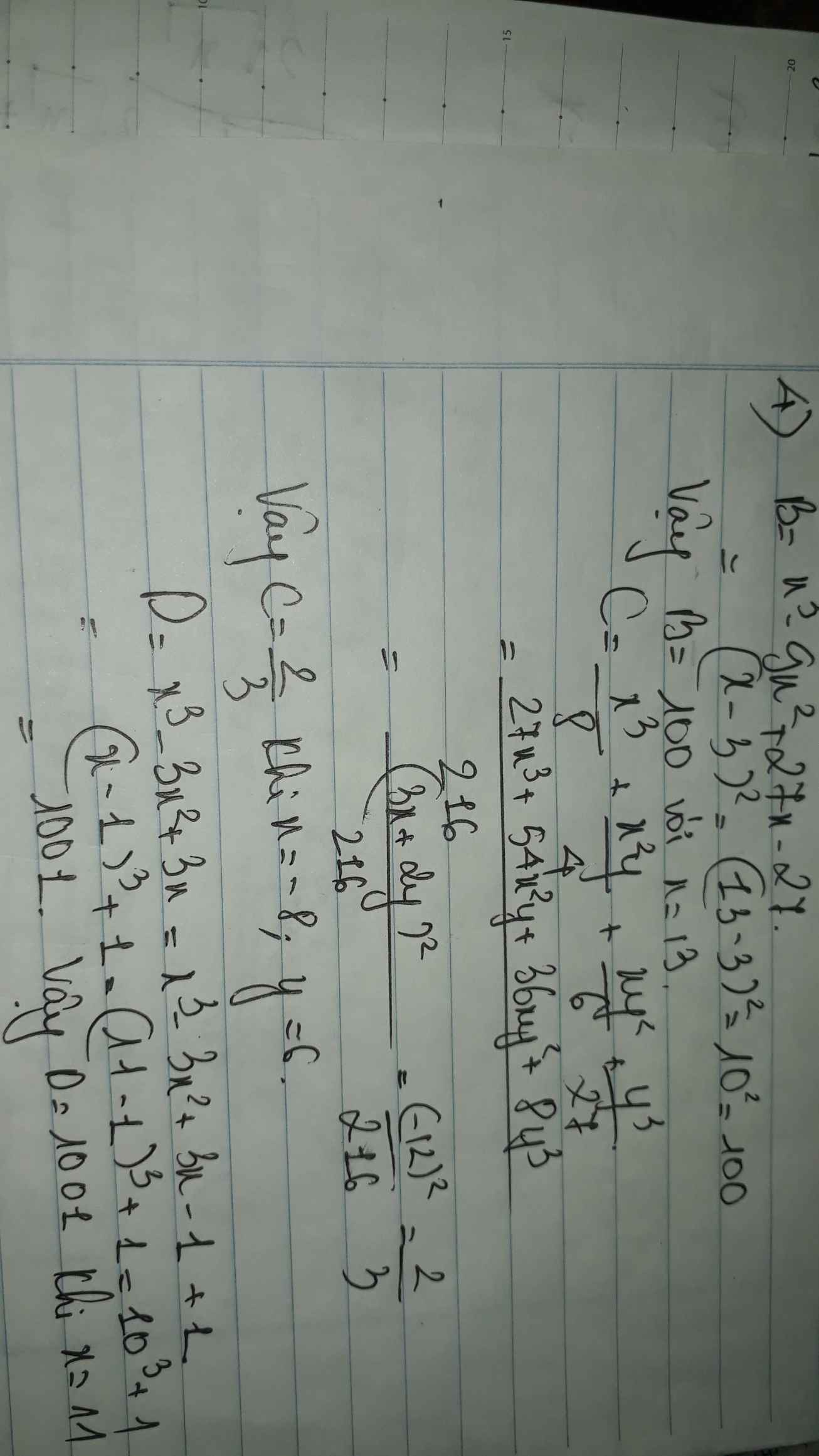


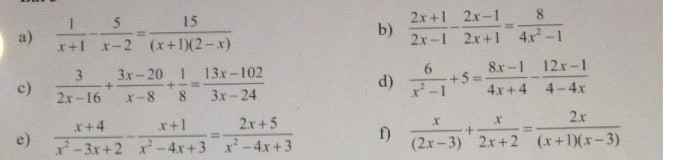
a: Xét ΔHAB có
I là trung điểm của HA
M là trung điểm của HB
Do đó: IM là đường trung bình của ΔHAB
Suy ra: IM//AB
hay ABMI là hình thang