
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

c: M>=0
=>x^2/(-x+6)>=0
=>-x+6>0
=>-x>-6
=>x<6
=>x<6 và \(x\notin\left\{0;3\right\}\)

\(1,=\left(x-y\right)\left(x^2+1\right)\\ 2,=\left(x+y\right)\left(2a-1\right)\\ 3,=x\left(x-y\right)+\left(x-y\right)=\left(x+1\right)\left(x-y\right)\\ 4,=\left(x-y\right)\left(x+y\right)-5\left(x+y\right)=\left(x+y\right)\left(x-y-5\right)\\ 5,=x\left(x-y\right)+2\left(x-y\right)=\left(x+2\right)\left(x-y\right)\\ 6,=5a\left(2x-y\right)-\left(2x-y\right)=\left(5a-1\right)\left(2x-y\right)\)

c: Gọi bốn số nguyên liên tiếp là x;x+1;x+2;x+3
Ta có: \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+3x\right)\left(x^2+3x+2\right)+1\)
\(=\left(x^2+3x\right)^2+2\left(x^2+3x\right)+1\)
\(=\left(x^2+3x+1\right)^2\)
\(d,M=\left(x^2-4xy+4y^2\right)-2\left(x-2y\right)+1+9\\ M=\left(x-2y\right)^2-2\left(x-2y\right)+1+9\\ M=\left(x-2y+1\right)^2+9\ge9\\ M_{min}=9\Leftrightarrow x=2y-1\)

2: \(ax+ay+bx+by\)
\(=a\left(x+y\right)+b\left(x+y\right)\)
\(=\left(x+y\right)\left(a+b\right)\)
3: \(x\left(x-2y\right)-x+2y\)
\(=x\left(x-2y\right)-\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x-1\right)\)

Ta có : n^3 - n (n € Z )
= n(n^2 -1)
=n(n-1)(n+1)
=(n-1)n(n+1)
mà n-1 ; n ; n+1 là 3 số nguyên liên tiếp nên sẽ có 1 số chia hết cho 2 và một số chia hết cho 3
=> (n-1)n(n+1) chia hết cho 2 và 3
=> (n-1)n(n+1) chia hết cho 2.3
=> (n-1)n(n+1) chia hết cho 6 (đpcm)

\(=\frac{\left(x^3\right)^2-\left(y^3\right)^2}{\left[\left(x^2\right)^2-\left(y^2\right)^2\right]-xy\left(x^2-y^2\right)}=\)
\(=\frac{\left(x^3-y^3\right)\left(x^3+y^3\right)}{\left(x^2-y^2\right)\left(x^2+y^2\right)-xy\left(x^2-y^2\right)}=\)
\(=\frac{\left(x+y\right)\left(x^2-xy+y^2\right)\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x^2-y^2\right)\left(x^2+y^2-xy\right)}=\)
\(=\frac{\left(x^2-y^2\right)\left(x^2-xy+y^2\right)\left(x^2+xy+y^2\right)}{\left(x^2-y^2\right)\left(x^2-xy+y^2\right)}=x^2+xy+y^2\)


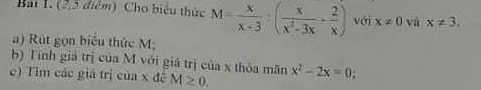 giúp mình câu c với ạ (câu a đáp án là
giúp mình câu c với ạ (câu a đáp án là 
Bài 6:
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
a)xét hai tam giác vuông △ABC và △HBA có
\(\widehat{ABC}=\widehat{ABH}\left(=90^0\right)\)
\(\widehat{H}\) chung
Do đó △ABC ∼ △ABH (g-g)