giúp mình câu 5 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
S
7 tháng 11 2023
\(\sqrt{4x-5}=\sqrt{3}\) (ĐKXĐ: \(x\ge\dfrac{5}{4}\))
\(\Rightarrow4x-5=3\)
\(\Rightarrow4x=8\)
\(\Rightarrow x=2\)(thỏa mãn)
Vậy x = 2
#gboy2mai
7 tháng 11 2023
\(\sqrt{4x-5}=\sqrt{3}\left(ĐKXĐ:x\ge\dfrac{5}{4}\right)\)
\(\Rightarrow4x-5=3\)
\(\Leftrightarrow4x=8\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy \(S=\left\{2\right\}\)
U
1
8 tháng 6 2021
Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....
6 tháng 5 2022
2.c
\(x+\sqrt{4x^2-4x+1}=5\)
\(\Leftrightarrow x+\sqrt{\left(2x-1\right)^2}=5\)
\(\Leftrightarrow x+\left|2x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2x-1=5;x\ge\dfrac{1}{2}\\x+1-2x=5;x< \dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}3x=6\\-x=4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=-4\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{2;-4\right\}\)
TM
6 tháng 4 2023
Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
TM
6 tháng 4 2023
Bài IV.b.
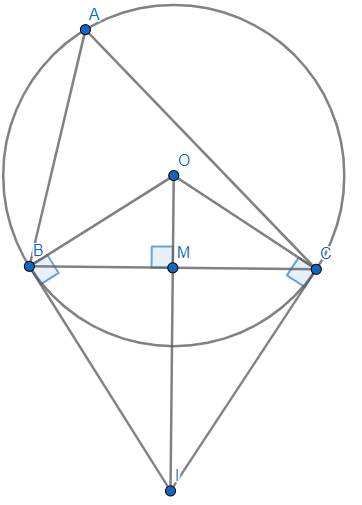
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
18 tháng 9 2023
a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)
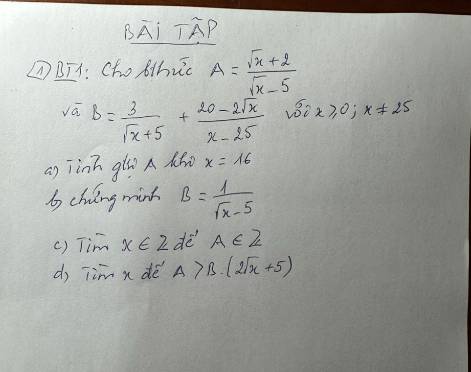
Câu 5:
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC tại H và H là trung điểm của BC
b: Xét (O) có
ΔCED nội tiếp
CD là đường kính
Do đó; ΔCED vuông tại E
=>CE\(\perp\)ED tại E
=>CE\(\perp\)AD tại E
Xét ΔDCA vuông tại C có CE là đường cao
nên \(DA\cdot DE=DC^2=\left(2R\right)^2=4R^2\left(3\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
=>\(4\cdot OH\cdot OA=4\cdot OB^2=\left(2OB\right)^2=4R^2\left(4\right)\)
Từ (3) và (4) suy ra \(DA\cdot DE=4\cdot OH\cdot OA\)