K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
20 tháng 5 2021
Mình nghĩ những câu tính một chút là ra ngay như này ko cần bấm máy tính đâu, có khi nó lại tốn t/g hơn ngồi tính đấy :v
\(=\int\left(1-\dfrac{1}{\cos^2x}\right)d\left(\cos x\right)\)
\(u=\cos x\Rightarrow....=\int du-\int\dfrac{du}{u^2}=u+\dfrac{1}{u}=\cos x+\dfrac{1}{\cos x}\)
\(\Rightarrow\int\limits^{\dfrac{\pi}{4}}_0...=\cos\dfrac{\pi}{4}-\cos0+\dfrac{1}{\cos\dfrac{\pi}{4}}-\dfrac{1}{\cos0}=\dfrac{3}{\sqrt{2}}+2.\left(-1\right)\)
\(\Rightarrow a^4-b^4=3^4-1=80\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
23.
Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)
(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)
\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)
Khi đó:
\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))
\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)
\(\Leftrightarrow M\) trùng I
\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
24.
\(a+b=4\Rightarrow b=4-a\)
ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow C\left(a;a;0\right)\)
Tương tự ta có: \(C'\left(a;a;b\right)\)
M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)
Theo công thức tích có hướng:
\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)
\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)
\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)
Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)
\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
84.
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) đồng thời SB là hình chiếu vuông góc của SC lên (SAB)
\(\Rightarrow\widehat{BSC}\) là góc giữa SC và (SAB)
\(\Rightarrow\widehat{BSC}=30^0\)
\(\Rightarrow SB=\dfrac{BC}{tan30^0}=a\sqrt{3}\)
\(\Rightarrow SA=\sqrt{SB^2-AB^2}=a\sqrt{2}\)
\(V=\dfrac{1}{3}SA.BC^2=\dfrac{a^3\sqrt{2}}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
87.
Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\) (trung tuyến đồng thời là đường cao trong tam giác cân)
Mà \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAM\right)\)
Lại có BC là giao tuyến (SBC) và (ABC)
\(\Rightarrow\widehat{SMA}\) là góc giữa (SBC) và (ABC)
\(\Rightarrow\widehat{SMA}=60^0\)
\(AM=\sqrt{AB^2-BM^2}=\sqrt{4a^2-\left(\dfrac{3a}{2}\right)^2}=\dfrac{a\sqrt{7}}{2}\)
\(SA=AM.tan60^0=\dfrac{a\sqrt{21}}{2}\)
\(V=\dfrac{1}{3}SA.\dfrac{1}{2}.AM.BC=\dfrac{7a^3\sqrt{3}}{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
AH
Akai Haruma
Giáo viên
14 tháng 10 2023
Lời giải:
\(y'=\frac{1-m}{(x+1)^2}\)
Nếu $m=1$ thì $y=1$ với mọi $x\neq -1$ (loại)
Nếu $m> 1$ thì hàm số nghịch biến trên TXĐ
$\Rightarrow$ với $x\in [0;1]$ thì:
$y_{\min}=y(1)=\frac{m+1}{2}=3$
$\Leftrightarrow m=5$
Nếu $m<1$ thì hàm số đồng biến trên TXĐ
$\Rightarrow$ với $x\in [0;1]$ thì:
$y_{\min}=y(0)=\frac{0+m}{0+1}=3\Leftrightarrow m=3$ (vô lý do $m< 1$)
Vậy $m=5$. Nghĩa là đáp án D đúng.
15 tháng 10 2023
\(g'\left(x\right)=\left(-2x\right)'\cdot f'\left(-2x\right)\)
\(=-2\cdot f'\left(-2x\right)\)
\(=-2\left(-2x^2-4x\right)\)
\(=4x^2+8x\)
\(g''\left(x\right)=4\cdot2x+8=8x+8\)
g'(x)=0
=>4x(x+2)=0
=>x=0 hoặc x=-2
Khi x=0 thì \(g''\left(x\right)=8\cdot0+8=8\)>0
=>Khi x=0 thì g(x) đạt giá trị cực đại
Khi x=-2 thì \(g''\left(x\right)=8\cdot\left(-2\right)+8=-8< 0\)
=>Khi x=-2 thì g(x) không đạt giá trị cực đại
Vậy: G(x) đạt giá trị cực đại tại x=0
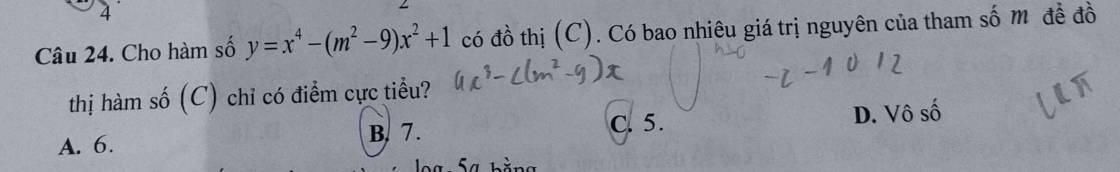
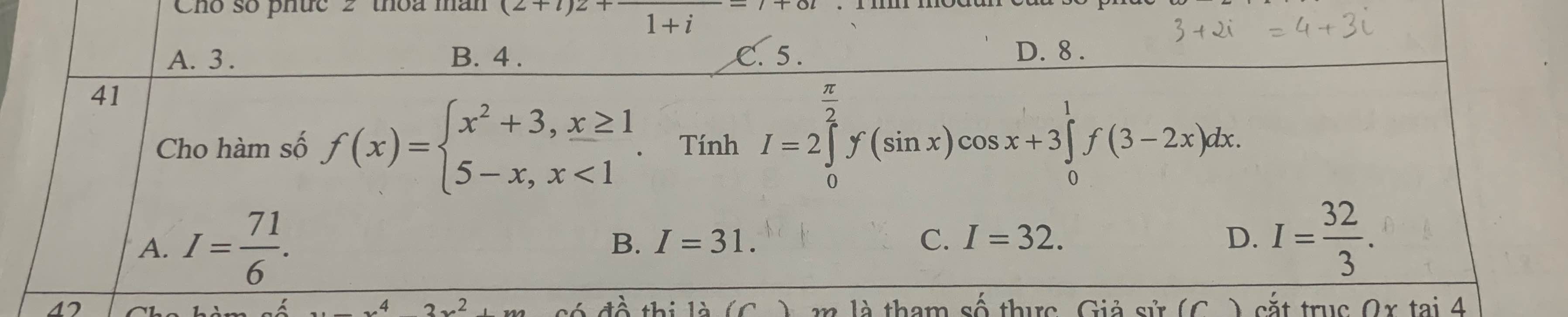
Lời giải:
Với hệ số lớn nhất là $1>0$ thì hàm trùng phương chỉ có cực tiểu khi mà:
$y'=4x^3-2(m^2-9)x=0$ có 1 nghiệm duy nhất.
$\Leftrightarrow 2x[2x^2-(m^2-9)]=0$ có nghiệm duy nhất. (*)
Mà pt này đã có sẵn nghiệm $x=0$ nên (*) xảy ra khi mà $2x^2-(m^2-9)=0$ vô nghiệm hoặc có nghiệm $x=0$
$\Leftrightarrow m^2-9=0$ hoặc $m^2-9<0$
$\Leftrightarrow m^2\leq 9$
$\Leftrightarrow -3\leq m\leq 3$
$\Leftrightarrow m\in\left\{-3; -2; -1; 0; 1; 2; 3\right\}$
Tức là có 7 giá trị $m$ nguyên tm.