Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{2}\sqrt{4-\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)



\(a,ĐKXĐ:\left\{{}\begin{matrix}8-4x\ge0\\5x-10\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le2\\x\ne2\end{matrix}\right.\Leftrightarrow x< 2\\ b,ĐKXĐ:\left\{{}\begin{matrix}\dfrac{-3}{x+2}\ge0\\x^2+2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2< 0\left(-3< 0;x+2\ne0\right)\\x\in R\left(x^2+2\ge2>0\right)\end{matrix}\right.\Leftrightarrow x< -2\)

a: Xét tứ giác BGCK có
M là trung điểm chung của BG và CK
=>BGCK là hbh
=>BG//CK và BK//CG
=>BK vuông góc AB và CK vuông góc CA
góc ABK+góc ACK=90+90=180 độ
=>ABKC nội tiếp đường tròn đường kính AK
=>K thuộc (O)
b:AK là đường kính của (O)
=>O là trung điểm của AK
Xét ΔAKG có
KO/KA=KM/KG
=>OM//AG và OM/AG=KM/KG=1/2
=>AG=2OM

\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...

\(A=\left(4x^2+2\cdot2\cdot\dfrac{1}{4}x+\dfrac{1}{16}\right)-\dfrac{1}{16}=\left(2x+\dfrac{1}{4}\right)^2-\dfrac{1}{16}\ge-\dfrac{1}{16}\\ A_{min}=-\dfrac{1}{16}\Leftrightarrow2x+\dfrac{1}{4}=0\Leftrightarrow x=-\dfrac{1}{8}\)

\(P=\dfrac{2\sqrt{x}+1+\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+1+1-x}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{-x+2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}=\dfrac{-x+2\sqrt{x}+2}{x+3\sqrt{x}+2}\)
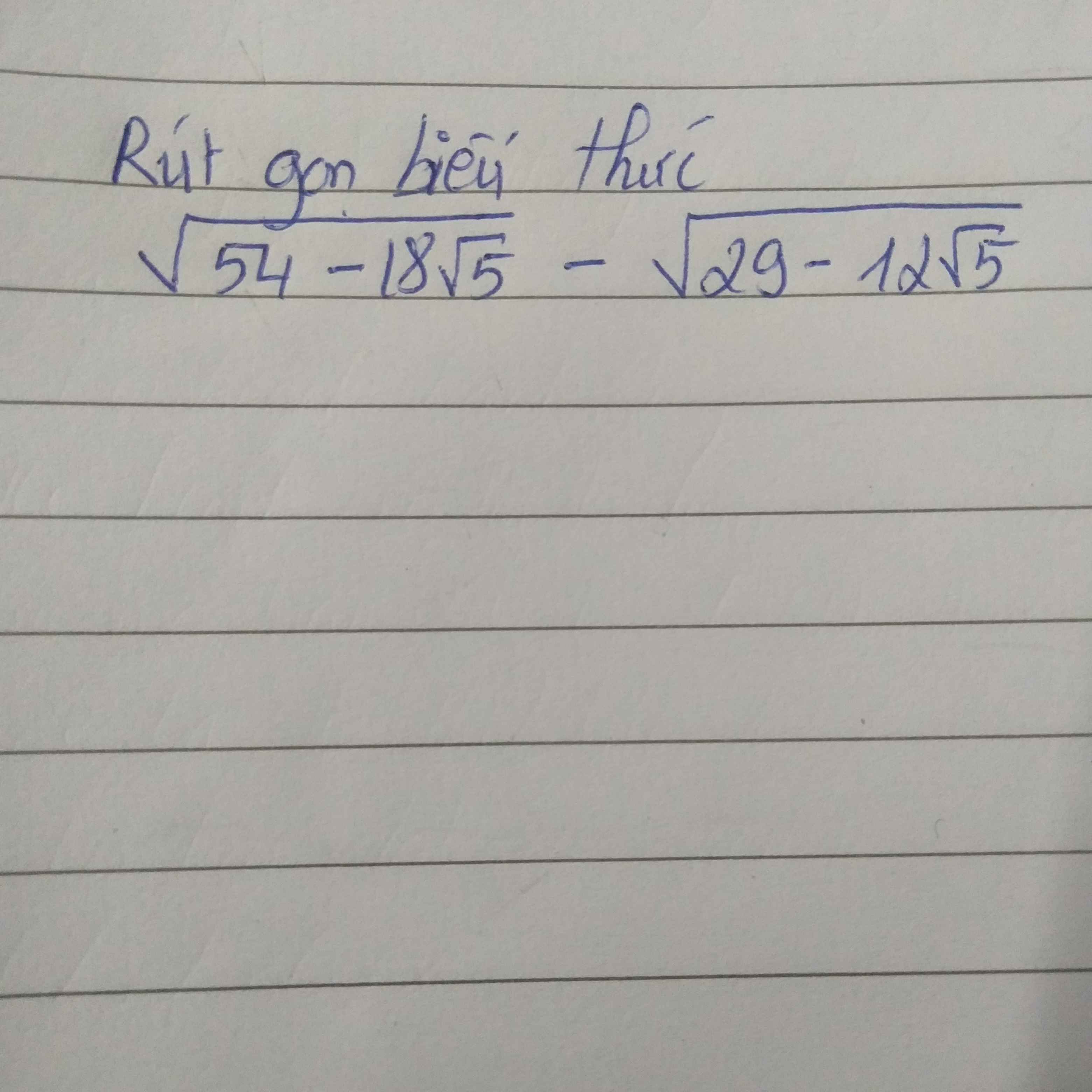
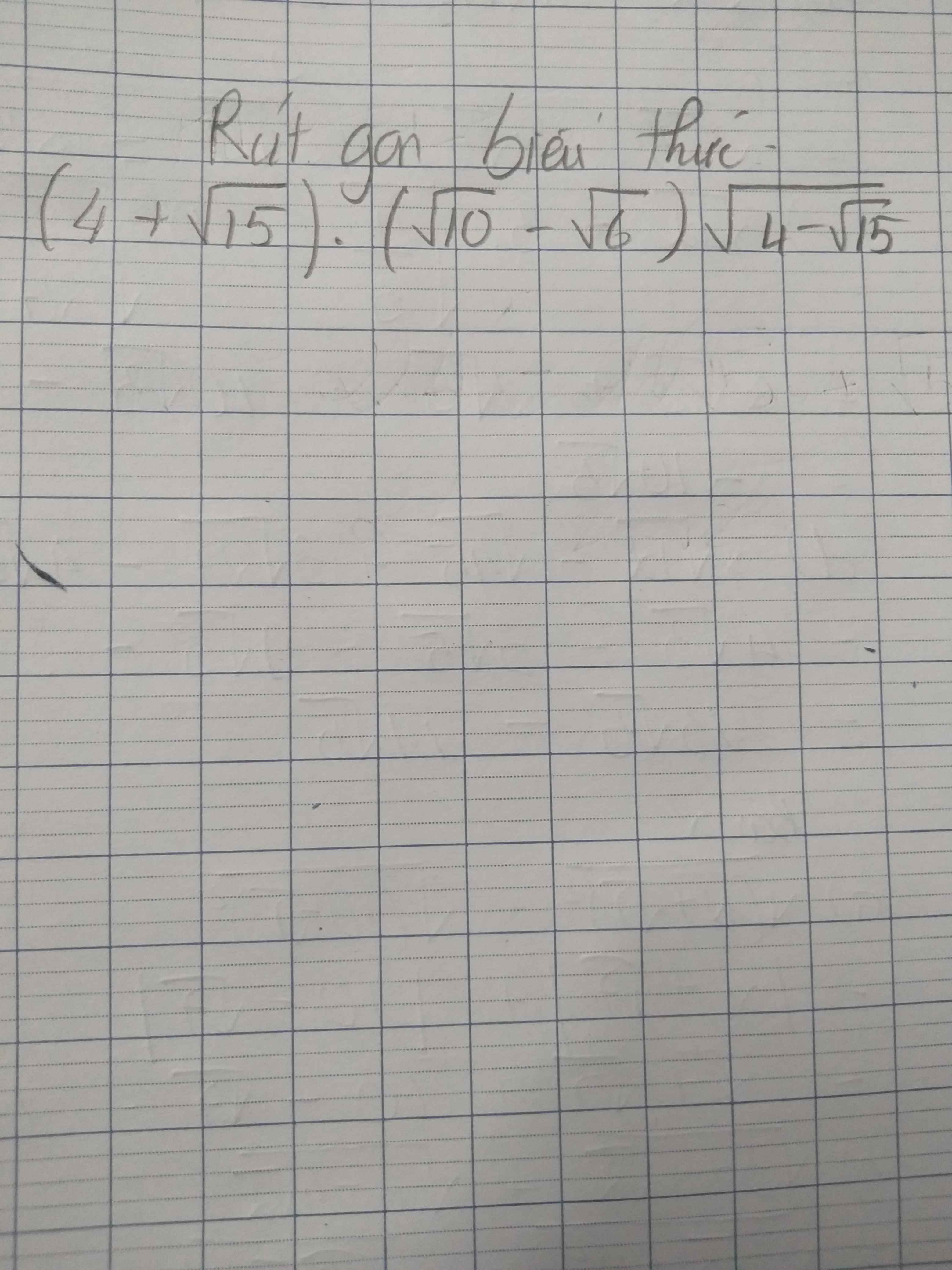

 Ai giúp mình giải câu 3 với,mình cảm ơn nhìuuuu ạ 🥺
Ai giúp mình giải câu 3 với,mình cảm ơn nhìuuuu ạ 🥺