
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi

1:
a: =>(x-1)(x-7)=0
=>x=1 hoặc x=7
b: =>x(x^2-9x+8)=0
=>x(x-1)(x-8)=0
=>\(x\in\left\{0;1;8\right\}\)
c: Đặt 1/căn x-7=a; 1/căn y+6=b
Theo đề, ta có:
7a-4b=5/3 và 5a+3b=13/6
=>a=1/3 và b=1/6
=>x-7=9 và y+6=36
=>x=16 và y=30
Bài 3:
a: Δ=(2m+3)^2-4(m^2+3m+2)
=4m^2+12m+9-4m^2-12m-8=1>0
=>PT luôn có hai nghiệm pb
b: x1^2+x2^2=1
=>(x1+x2)^2-2x1x2=1
=>(2m+3)^2-2(m^2+3m+2)=1
=>4m^2+12m+9-2m^2-6m-4-1=0
=>2m^2+6m+4=0
=>m=-1 hoặc m=-2

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó:AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA⊥BC
Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp

Phương trình (D) có dạng:
\(y=k\left(x-1\right)-2\Leftrightarrow y=kx-k-2\)
Phương trình hoành độ giao điểm (P) và (D):
\(-\dfrac{x^2}{4}=kx-k-2\Leftrightarrow x^2+4kx-4\left(k+2\right)=0\) (1)
\(\Delta'=4k^2+4\left(k+2\right)=\left(2k+1\right)^2+7>0\) ; \(\forall k\)
\(\Rightarrow\) (1) luôn có 2 nghiệm pb hay (D) luôn cắt (P) tại 2 điểm pb A và B
b. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-4k\\x_Ax_B=-4\left(k+2\right)\end{matrix}\right.\)
Đặt \(A=x_A^2x_B+x_Ax_B^2=x_Ax_B\left(x_A+x_B\right)\)
\(A=-4\left(k+2\right).\left(-4k\right)=16\left(k^2+2k\right)=16\left(k+1\right)^2-16\ge-16\)
\(\Rightarrow A_{min}=-16\) khi \(k+1=0\Leftrightarrow k=-1\)

Bài 5:
Xét ΔADC vuông tại D có DO là đường cao ứng với cạnh huyền AC
nên \(\left\{{}\begin{matrix}AD^2=AO\cdot AC\\DC^2=CO\cdot CA\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AO=7,2\left(cm\right)\\CO=12,8\left(cm\right)\end{matrix}\right.\)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành

a: Thay \(x=9+4\sqrt{2}\) vào A, ta được:
\(A=\dfrac{2\sqrt{2}+1+7}{2\sqrt{2}+1-1}=\dfrac{8+2\sqrt{2}}{2\sqrt{2}}=2\sqrt{2}+1\)
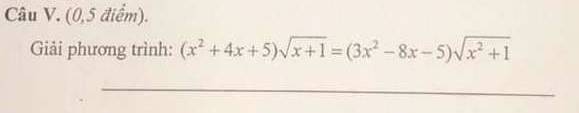



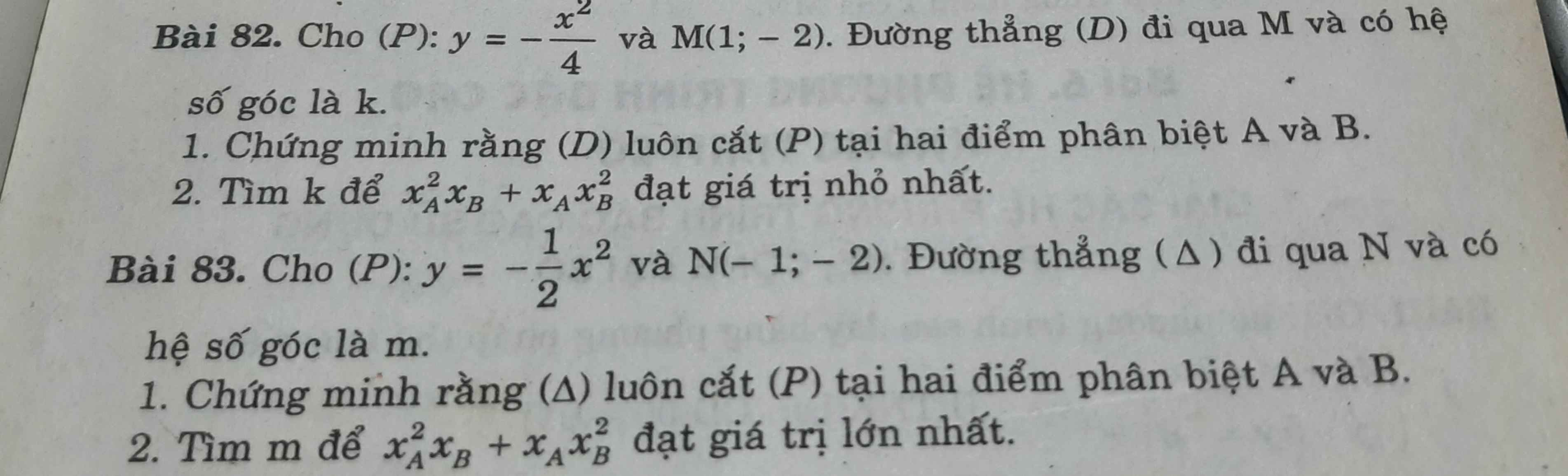


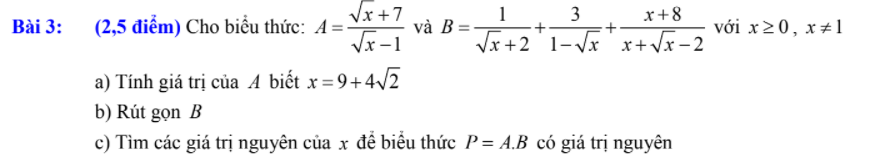 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
ĐKXĐ :\(\left\{{}\begin{matrix}x+1\ge0\\x^2+1\ge0\end{matrix}\right.\Leftrightarrow x\ge-1\)
Khi đó \((x^2+4x+5)\sqrt{x+1}=(3x^2-8x-5)\sqrt{x^2+1}\)
\(\Leftrightarrow(x^2+1)\sqrt{x+1}+4(x+1)\sqrt{x+1}=3(x^2+1)\sqrt{x^2+1}-8(x+1)\sqrt{x^2+1}\)
Đặt \(\sqrt{x+1}=a;\sqrt{x^2+1}=b(a\ge0;b>0)\)
Phương trình trở thành :
\(4a^3+ab^2=3b^3-8a^2b\)
\(\Leftrightarrow4(a^3+b^3)+b(8a^2+ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2-4ab+4b^2)+(a+b)(8ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2+4ab-3b^2)=0\)
\(\Leftrightarrow\left(a+b\right)\left(2a-b\right)\left(2a+3b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0(\text{loại})\\2a-b=0\\2a+3b=0(\text{loại})\end{matrix}\right.\Leftrightarrow2a=b\) (vì \(\left\{{}\begin{matrix}a\ge0\\b>0\end{matrix}\right.\) nên a+b>0 ; 2a +3b > 0)
Trở lại cách đặt ta được
\(2\sqrt{x+1}=\sqrt{x^2+1}\Leftrightarrow x^2-4x-3=0\)
\(\Leftrightarrow x=\pm\sqrt{7}+2\) (loại \(x=-\sqrt{7}+2\))
Vậy x = \(\sqrt{7}+2\) là nghiệm phương trình