
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) đk \(x\ge\dfrac{-3}{2}\)
PT <=> \(4x^2\left(2x+3\right)=\left(3x^2+6x+1\right)^2\)
<=> \(8x^3+12x^2=9x^4+36x^2+1+36x^3+12x+6x^2\)
<=> \(9x^4+28x^3+30x^2+12x+1=0\)
<=> \(\left(x+1\right)^3\left(9x+1\right)=0\)
<=> \(\left[{}\begin{matrix}x=-1\left(c\right)\\x=\dfrac{-1}{9}\left(l\right)\end{matrix}\right.\)
KL: PT có nghiệm duy nhất x = -1
b) đk: \(x\ge-1;x\ge2y\)
hpt <=> \(\left\{{}\begin{matrix}2x^2-4xy+3y-4x-4=\sqrt{9\left(x-1\right)\left(x+1\right)\left(x-2y\right)}\left(1\right)\\2x-2y+1+2\sqrt{\left(x+1\right)\left(x-2y\right)}=2x-2y+5\left(2\right)\end{matrix}\right.\)
(2) <=> \(\sqrt{\left(x+1\right)\left(x-2y\right)}=2\)
<=> \(\left(x+1\right)\left(x-2y\right)=4\)
(1) <=> 2(x+1)(x-2y) + x - 4 = \(6.\sqrt{x-1}\)
<=> x+4 = \(6\sqrt{x-1}\)
<=> x2 + 8x + 16 = 36x - 36
<=> x2 -28x + 52 = 0
<=> (x-26)(x-2) = 0
<=> \(\left[{}\begin{matrix}x=26< =>y=\dfrac{349}{27}\\x=2< =>y=\dfrac{1}{3}\end{matrix}\right.\)

22.
ĐKXĐ: \(y\ne1\)
\(\left\{{}\begin{matrix}x^2-\dfrac{1}{y-1}=2\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+\dfrac{2}{1-y}=4\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
Trừ pt dưới cho trên:
\(\Rightarrow\dfrac{1}{1-y}=-2\)
\(\Rightarrow1-y=-\dfrac{1}{2}\Rightarrow y=\dfrac{3}{2}\)
Thế vào \(x^2-\dfrac{1}{y-1}=2\)
\(\Rightarrow x^2=4\Rightarrow x=\pm2\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(2;\dfrac{3}{2}\right);\left(-2;\dfrac{3}{2}\right)\)
b.
ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
\(Hệ\Leftrightarrow\left\{{}\begin{matrix}2y^2-\dfrac{10}{2x+1}=8\\2y^2-\dfrac{11}{2x+1}=7\end{matrix}\right.\)
Trừ pt trên cho dưới:
\(\Rightarrow\dfrac{1}{2x+1}=1\)
\(\Rightarrow2x+1=1\)
\(\Rightarrow x=0\)
Thế vào \(y^2-\dfrac{5}{2x+1}=4\)
\(\Rightarrow y^2=9\Rightarrow y=\pm3\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(0;3\right);\left(0;-3\right)\)


`2x+5y=11(1)`
`2x-3y=0(2)`
Lấy (1) trừ (2)
`=>8y=11`
`<=>y=11/8`
`<=>x=(3y)/2=33/16`
a) Ta có: \(\left\{{}\begin{matrix}2x+5y=11\\2x-3y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y=11\\2x-3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{11}{8}\\2x=3y=3\cdot\dfrac{11}{8}=\dfrac{33}{8}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{33}{16}\\y=\dfrac{11}{8}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=\dfrac{33}{16}\\y=\dfrac{11}{8}\end{matrix}\right.\)
b) Ta có: \(\left\{{}\begin{matrix}4x+3y=6\\2x+y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\4x+2y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\2x+y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-2=4\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=6\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(3;-2)

Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.

Bài 1 : x² + x² -12 = 0
a = 1 , b = 1 , c = -12
∆ = 1 -4 × 1 × (-12)
∆ = 49 > 0 .✓49 =7
Vậy pt có 2 ng⁰ pb ( tự viết nhé ) !


Cô làm câu b thôi nhé :)
Ta có hệ \(\hept{\begin{cases}mx+4y=10-m\\x+my=4\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(4-my\right)+4y=10-m\\x=4-my\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(4-m^2\right)y=10-5m\left(1\right)\\x=4-my\end{cases}}\)
Với \(4-m^2=0\Leftrightarrow m=2\) hoặc \(m=-2\)
Xét m =2, phương trình (1) tương đương 0.x = 0. Vậy hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
Xét m = -2, phương trình (1) tương đương 0.x = 20. Vậy hệ phương trình vô nghiệm.
Với \(4-m^2\ne0\Leftrightarrow m\ne2\) và \(m\ne-2\), phương trình (1) tương đương \(y=\frac{10-5m}{4-m^2}=\frac{5}{2+m}\)
Từ đó : \(x=\frac{8-m}{2+m}\)
Kết luận:
+ m = 2, hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
+ m = - 2, hệ phương trình vô nghiệm.
+ \(m\ne2;m\ne-2\) hệ có 1 nghiệm duy nhất \(\hept{\begin{cases}x=\frac{8-m}{2+m}\\y=\frac{5}{2+m}\end{cases}}\)
Chúc em học tập tốt :)

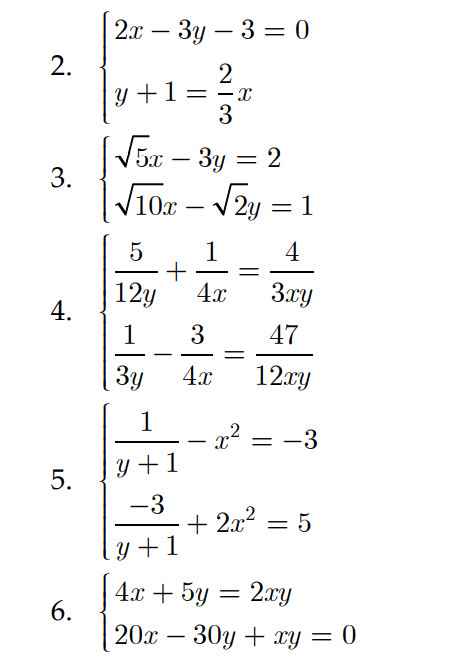
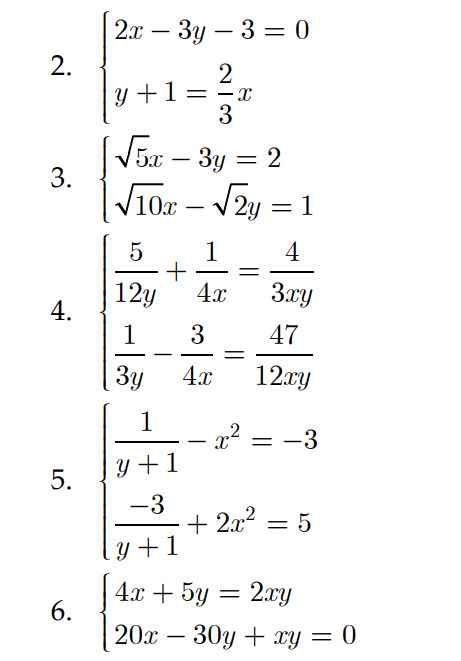

 mọi ng giải hộ em bài này với ạ( có lập bảng và giải bằng hệ phương trình ạ) e cần gấp
mọi ng giải hộ em bài này với ạ( có lập bảng và giải bằng hệ phương trình ạ) e cần gấp
Cách 1 :
\(\hept{\begin{cases}3x-2y=9\\x-3y=10\end{cases}\Leftrightarrow}\hept{\begin{cases}3x-2y=9\left(1\right)\\3x-9y=30\left(2\right)\end{cases}}\)
Trừ (1) và (2) ta được :
\(3x-2y-\left(3x-9y\right)=9-30\)
\(\Leftrightarrow3x-2y-3x+9y=-21\)
\(\Leftrightarrow7y=-21\Leftrightarrow y=-3\left(3\right)\)
Thay \(\left(3\right)\)vào \(\left(1\right)\) ta được :
\(3x-2y=9\Leftrightarrow3x-2\left(-3\right)=9\)
\(\Leftrightarrow3x+6=9\)
\(\Leftrightarrow3x=3\Leftrightarrow x=1\)
Cách 2 :
\(\hept{\begin{cases}3x-2y=9\\x-3y=10\end{cases}}\Leftrightarrow\hept{\begin{cases}2y=3x-9\\x-3y=10\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{3x-9}{2}\\x-3\cdot\frac{3x-9}{2}=10\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{3x-9}{2}\\x-\frac{9x-27}{2}=10\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{3x-9}{2}\\\frac{2x}{2}-\frac{9x-27}{2}=\frac{20}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{3x-9}{2}\\2x-9x+27=20\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{3x-9}{2}\\-7x=-7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{3\cdot1-9}{2}=-3\\x=1\end{cases}}\)
Vậy \(\left(x,y\right)=\left(1,-3\right)\)
C1 . Hệ phương trình \(\hept{\begin{cases}x=10+3y\\3\left(10+3y\right)-2y=9\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=10+3y\\30+9y-2y=9\end{cases}}\Leftrightarrow\hept{\begin{cases}x=10+3y\\y=-3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\end{cases}}\)
C2 : Hệ phương trình
\(\hept{\begin{cases}x=3+\frac{2}{3}y\\3+\frac{2}{3}y-3y=10\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3+\frac{2}{3}y\\y=-3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\end{cases}}\)