
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Gọi AC giao BD = I
Xét tam giác ADI có : AD = DI = AC
nên tam giác ADI là tam giác đều => ^IAD = ^ADI = 600
-> ^A = ^BAC + ^IAD = 800
Ta có : ^A + ^ADB + ^ABD = 1800 ( tổng 3 góc trong tam giác )
=> ^ABD = 1800 - ^A - ^ADB = \(180^0-80^0-60^0=40^0\)

Bài 2:
Áp dụng tc dtsbn:
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\widehat{A}=3\cdot12^0=36^0\)
Bài 3:
Gọi cd,cr lần lượt là a,b(cm;a,b>0)
Đặt \(\dfrac{a}{5}=\dfrac{b}{3}=k\left(k>0\right)\Rightarrow a=5k;b=3k\)
Mà \(ab=60\Rightarrow15k^2=60\Rightarrow k^2=4\Rightarrow k=2\)
\(\Rightarrow\left\{{}\begin{matrix}a=10\\b=6\end{matrix}\right.\)
Vậy chu vi hcn là \(2\left(a+b\right)=2\cdot16=32\left(cm\right)\)

5: góc BDC=góc BAC+góc ACD
=>góc BDC>góc BAC=60 độ=góc DBC
D nằm trên AB
=>CD nằm giữa CA và CB
góc BCD+góc ACD=góc ACB=60 độ
=>góc BCD<60 độ
=>góc BCD<góc DBC<góc BDC
=>BD<DC<BC

6) \(\dfrac{8^6}{256}=\dfrac{\left(2^3\right)^6}{2^8}=\dfrac{2^{18}}{2^8}=2^{10}=1024\)
7) \(\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{4}\right)^{20}=\left(\dfrac{1}{2}\right)^{15}.\left[\left(\dfrac{1}{2}\right)^2\right]^{20}=\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{2}\right)^{40}=\left(\dfrac{1}{2}\right)^{55}=\dfrac{1}{2^{55}}\)
8) \(\left(\dfrac{1}{9}\right)^{25}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{50}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{20}=\dfrac{1}{3^{20}}\)
9)\(\left(\dfrac{1}{16}\right)^3\div\left(\dfrac{1}{8}\right)^2=\left(\dfrac{1}{2}\right)^{12}\div\left(\dfrac{1}{2}\right)^6=\left(\dfrac{1}{2}\right)^6=\dfrac{1}{64}\)
10) \(\dfrac{27^2.8^5}{6^2.32^3}=\dfrac{3^6.2^{15}}{3^2.2^2.2^{15}}=\dfrac{3^4}{2^2}=\dfrac{81}{4}\)

a, bạn tự sắp xếp nhé
b, Ta có : \(P\left(x\right)+Q\left(x\right)\)hay
\(2x^5+3x^4-9x^3-2x^2-\dfrac{1}{4}x-2x^5+3x^4-2x^3+4x^2-\dfrac{1}{4}\)
\(=6x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
Ta có \(P\left(x\right)-Q\left(x\right)\)hay
\(2x^5+3x^4-9x^3-2x^2-\dfrac{1}{4}x+2x^5-3x^4+2x^3-4x^2+\dfrac{1}{4}\)
\(=4x^5-7x^3-6x^2-\dfrac{1}{4}x+\dfrac{1}{4}\)
Giá trị x=0 là nghiệm của P(x) vì ko có hệ số tự do => GT là 0
Cái còn lại 1/4 là hệ số tự do => x=0 ko phải là nghiệm của Q(x)
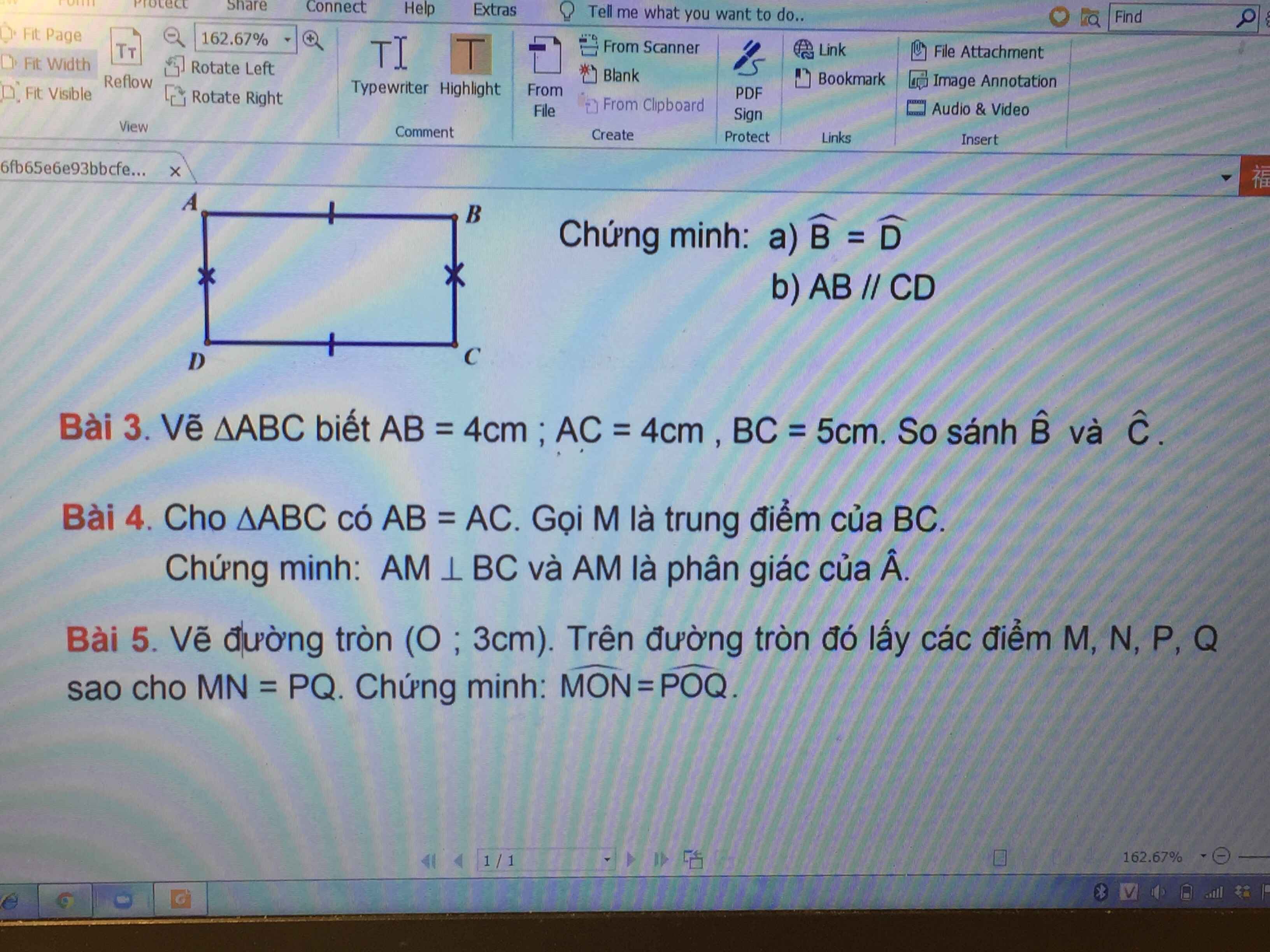
 giúp mình bài 5 với
giúp mình bài 5 với







TH1: \(a+b+c=0\Rightarrow\left\{{}\begin{matrix}a+b=-c\\b+c=-a\\c+a=-b\end{matrix}\right.\)
\(\Rightarrow\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{\left(-c\right).\left(-a\right).\left(-b\right)}{abc}=-1\)
TH2: \(a+b+c\ne0\)
Áp dụng dãy tỉ lệ thức bằng nhau:
\(\dfrac{a+b-c}{c}=\dfrac{c+a-b}{b}=\dfrac{b+c-a}{a}=\dfrac{a+b-c+c+a-b+b+c-a}{a+b+c}=1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b-c=c\\c+a-b=b\\b+c-a=a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\c+a=2b\\b+c=2a\end{matrix}\right.\)
\(\Rightarrow a=b=c\)
\(\Rightarrow\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{2a.2a.2a}{a^3}=8\)
Vậy biểu thức đã cho bằng -1 hoặc bằng 8