
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật

3:
c: Xét ΔCAM có KI//AM
nên KI/AM=CI/CM
Xét ΔCMB có HI//MB
nên HI/MB=CI/CM
=>KI/AM=HI/MB
=>KI=HI
=>I là trung điểm của HK

Bài 1:
Gọi x là số sản phẩm người thứ nhất làm được trong 1 ngày (sản phẩm)ư
(ĐK: 0 < x < 310)
Số sản phẩm 2 người làm được trong 1 ngày là:
930 : 3 = 310 (sản phẩm)
Vì 1 ngày người thứ nhất làm hơn người thứ 2 là 10 sản phẩm, nên số sản phẩm người thứ 2 làm trong 1 ngày là: x - 10
Vì tổng 2 người làm được 310 sản phẩm nên ta có phương trình:
x + (x - 10) = 310
<=> 2x - 10 = 310
<=> 2x = 320
<=> x = 160
Vậy số sản phẩm người thứ nhất làm được trong 1 ngày là 160 sản phẩm
Số sản phẩm người thứ 2 làm được trong 1 ngày là: 160 - 10 = 150 (sản phẩm)

Bài 1:
a: =5(x+2y)
b: =(x+y)(5x-7)
Bài 2:
a: \(=\dfrac{1+2}{xy}=\dfrac{3}{xy}\)

2.1
\(\Leftrightarrow x^3+3x^2+2x-3x^2-9x-6=0\)
\(=x\left(x^2+3x+2\right)-3\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\\x=-2\end{matrix}\right.\)
2.2
\(\Leftrightarrow x^3-2x^2-2x-x^2+2x+2=0\)
\(\Leftrightarrow x\left(x^2-2x-2\right)-\left(x^2-2x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-2x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=1\pm\sqrt{3}\end{matrix}\right.\)
2.3
\(\Leftrightarrow3x^3-3x^2+2x+3x^2-3x+2=0\)
\(\Leftrightarrow x\left(3x^2-3x+2\right)+3x^2-3x+2=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2-3x+2\right)=0\)
\(\Leftrightarrow x=-1\)
2.5
\(\Leftrightarrow2x^3+x^2+3x-4x^2-2x-6=0\)
\(\Leftrightarrow x\left(2x^2+x+3\right)-2\left(2x^2+x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x^2+x+3\right)=0\)
\(\Leftrightarrow x=2\)

Bài 3:
b: Ta có: CD=CN
mà CN=BM
nên CD=BM
Xét ΔABC có
\(\dfrac{BM}{BA}=\dfrac{CD}{CA}\)
nên MD//BC
Xét tứ giác BMDC có MD//BC
nên BMDC là hình thang
mà \(\widehat{MBC}=\widehat{DCB}\)
nên BMDC là hình thang cân

a: Xét tứ giác ABMD có
\(\widehat{BMD}=\widehat{BAD}=\widehat{ADM}=90^0\)
Do đó: ABMD là hình chữ nhật
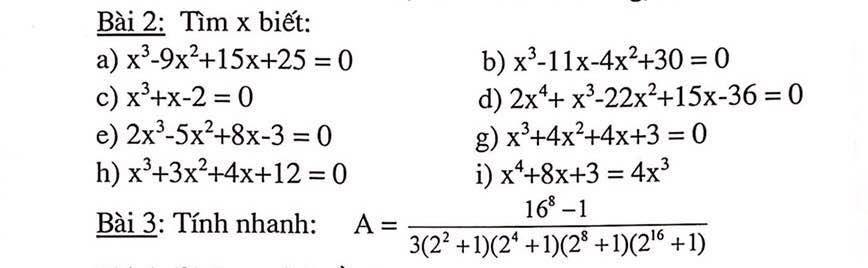







 bài 2 câu 1,2,3,5,9
bài 2 câu 1,2,3,5,9 

h: Ta có: \(x^3+3x^2+4x+12=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2+4\right)=0\)
\(\Leftrightarrow x+3=0\)
hay x=-3