K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
24 tháng 8 2023
Bài 1:
a)
\(A=\sqrt{2}\left(\sqrt{4.2}-\sqrt{16.2}+3\sqrt{9.2}\right)\\ =\sqrt{2}\left(2\sqrt{2}-4\sqrt{2}+9\sqrt{2}\right)\\ =\sqrt{2}.7\sqrt{2}\\ =7\)
b)
\(B=\dfrac{5\left(\sqrt{6}-1\right)\left(\sqrt{6}-1\right)}{6-1}+\dfrac{\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}-\sqrt{3}\right)}{2-3}+\sqrt{\sqrt{2}^2-2.\sqrt{2}.\sqrt{1}+\sqrt{1}^2}\\ =\dfrac{5\left(\sqrt{6}-1\right)^2}{5}-\left(\sqrt{2}-\sqrt{3}\right)^2+\sqrt{\left(\sqrt{2}-1\right)^2}\\ =5\left(6-2\sqrt{6}+1\right)-\left(2-2\sqrt{6}+3\right)+\sqrt{2}-1\\ =30-10\sqrt{6}+5-2+2\sqrt{6}-3+\sqrt{2}-1\\ =29-8\sqrt{6}\)
25 tháng 8 2023
2:
a: \(\sqrt{x^2-2x+9}=x+2\)
=>x>=-2 và x^2-2x+9=x^2+4x+4
=>x>=-2 và -2x+9=4x+4
=>x>=-2 và -6x=-5
=>x=5/6(nhận)
b:
ĐKXĐ: x^2-4>=0 và x+2>=0
=>x>=-2 và (x>=2 hoặc x<=-2)
=>x=-2 hoặc x>=2
\(\sqrt{x^2-4}+\sqrt{x+2}=0\)
=>x^2-4=0 và x+2=0
=>x=-2
c:
ĐKXĐ: x>=1
\(\sqrt{x+3-4\sqrt{x-1}}=3\)
=>\(\sqrt{x-1-2\cdot\sqrt{x-1}\cdot2+4}=3\)
=>\(\left|\sqrt{x-1}-2\right|=3\)
=>\(\left[{}\begin{matrix}\sqrt{x-1}-2=3\\\sqrt{x-1}-2=-3\end{matrix}\right.\Leftrightarrow\sqrt{x-1}=5\)
=>x-1=25
=>x=26
d: \(\sqrt{4-8x}-4\sqrt{1-2x}+\sqrt{\dfrac{9-18x}{4}}+1=0\)
=>\(2\sqrt{1-2x}-4\sqrt{1-2x}+\dfrac{3}{2}\sqrt{1-2x}+1=0\)
=>\(1-\dfrac{1}{2}\sqrt{1-2x}=0\)
=>\(\sqrt{1-2x}=2\)
=>1-2x=4
=>2x=-3
=>x=-3/2
P
1
8 tháng 11 2021
Bài 1:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+5\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
8 tháng 11 2021
Bài 1:
\(b,\) PTHDGD là \(x+2=-2x+5\Leftrightarrow x=1\Leftrightarrow y=3\Leftrightarrow A\left(1;3\right)\)
Vậy A(1;3) là giao điểm 2 đths
\(c,\) PT giao Ox là \(y=0\Leftrightarrow x=-2\Leftrightarrow B\left(-2;0\right)\Leftrightarrow OB=\left|-2\right|=2\)
PT giao Oy là \(x=0\Leftrightarrow y=-2\Leftrightarrow C\left(0;-2\right)\Leftrightarrow OC=\left|-2\right|=2\)
Do đó \(\tan\widehat{OBC}=\dfrac{OC}{OB}=1\Leftrightarrow\widehat{OBC}=45^0\)
Mà hệ số a của đt >0 nên góc tạo bởi đt với Ox là góc nhọn có sđ 45o
NA
1
3 tháng 7 2021
\(A=\dfrac{\sqrt{3x-9}}{x}=\sqrt{\dfrac{3x-9}{x^2}}=\sqrt{-\dfrac{9}{x^2}+\dfrac{3}{x}}\)\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{9}{x^2}+2.\dfrac{3}{x}.\dfrac{1}{2}+\dfrac{1}{4}\right)}\)
\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{3}{x}-\dfrac{1}{2}\right)^2}\le\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(\dfrac{3}{x}-\dfrac{1}{2}=0\Leftrightarrow x=6\) (tm)
Vậy \(A_{max}=\dfrac{1}{2}\)
\(B=\dfrac{\sqrt{2x-4}}{x}=\sqrt{\dfrac{2x-4}{x^2}}=\sqrt{-\dfrac{4}{x^2}+\dfrac{2}{x}}=\sqrt{\dfrac{1}{4}-\left(\dfrac{4}{x^2}-2.\dfrac{2}{x}.\dfrac{1}{2}+\dfrac{1}{4}\right)}\)
\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{2}{x}-\dfrac{1}{2}\right)^2}\le\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(\dfrac{2}{x}-\dfrac{1}{2}=0\Leftrightarrow x=4\) (tm)
Vậy \(B_{max}=\dfrac{1}{2}\)
\(C=\dfrac{\sqrt{x-4}}{3x}=\sqrt{\dfrac{x-4}{9x^2}}=\sqrt{-\dfrac{4}{9x^2}+\dfrac{1}{9x}}=\sqrt{\dfrac{1}{144}-\left(\dfrac{4}{9x^2}-2.\dfrac{2}{3x}.\dfrac{1}{12}+\dfrac{1}{144}\right)}\)
\(=\sqrt{\dfrac{1}{144}-\left(\dfrac{2}{3x}-\dfrac{1}{12}\right)^2}\le\sqrt{\dfrac{1}{144}}=\dfrac{1}{12}\)
Dấu "=" xảy ra khi \(x=8\) (tm)
Vậy \(C_{max}=\dfrac{1}{12}\)
7 tháng 9 2021
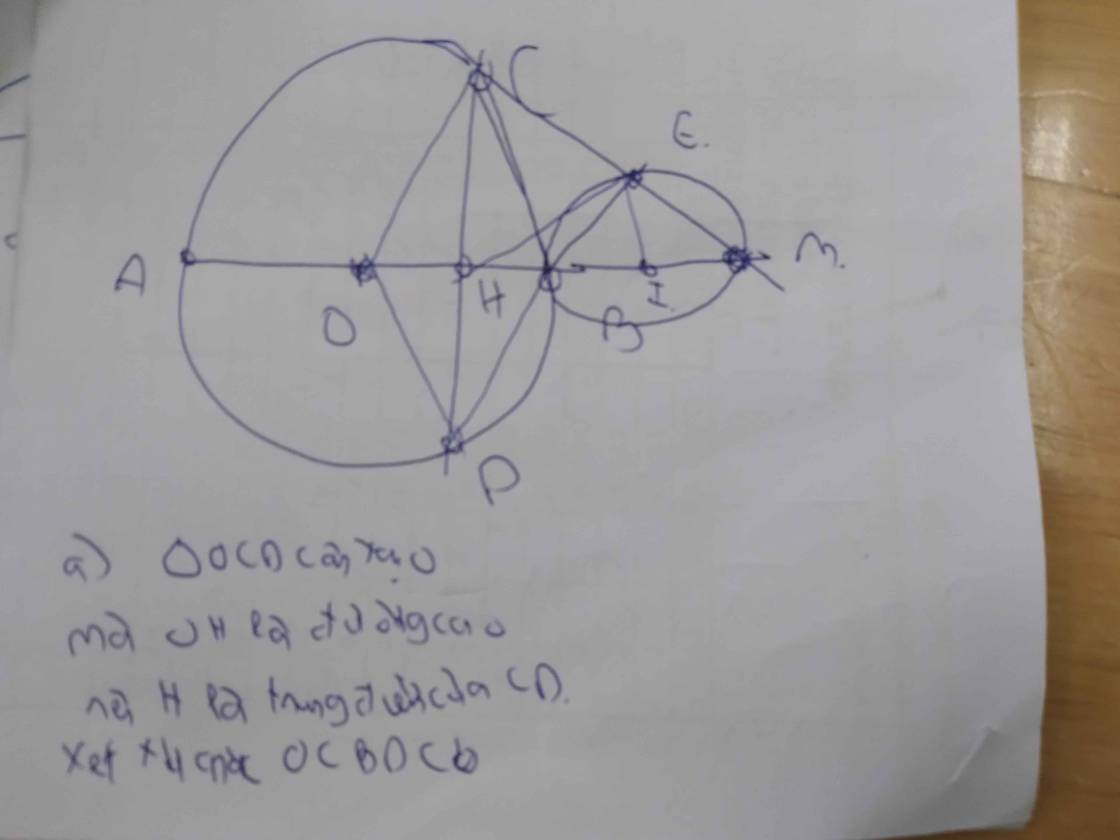
\(a,\) Ta có \(OA=OB=OC=R=\dfrac{1}{2}AB\Rightarrow\Delta ABC\perp C\)
\(b,CB=\sqrt{AB^2-AC^2}=\sqrt{\left(AO+OB\right)^2-AC^2}\\ =\sqrt{20^2-10^2}=10\sqrt{3}\left(cm\right)\)
Ta có \(CA=R=CO\Rightarrow\Delta ACO\) đều
\(\Rightarrow\widehat{CAO}=\widehat{ACO}=\widehat{COA}=60\)
\(\Rightarrow\widehat{ABC}=90-\widehat{CAO}=90-60=30\)
và \(\widehat{ACB}=90\left(\Delta ABC\perp C\right)\)
\(c,\) Áp dụng HTL tam giác ABC vuông tại C có đường cao CH:
\(CH\cdot AB=AC\cdot AB\Leftrightarrow CH\cdot20=10\cdot10\sqrt{3}\\ \Leftrightarrow CH=\dfrac{100\sqrt{3}}{20}=5\sqrt{3}\left(cm\right)\)
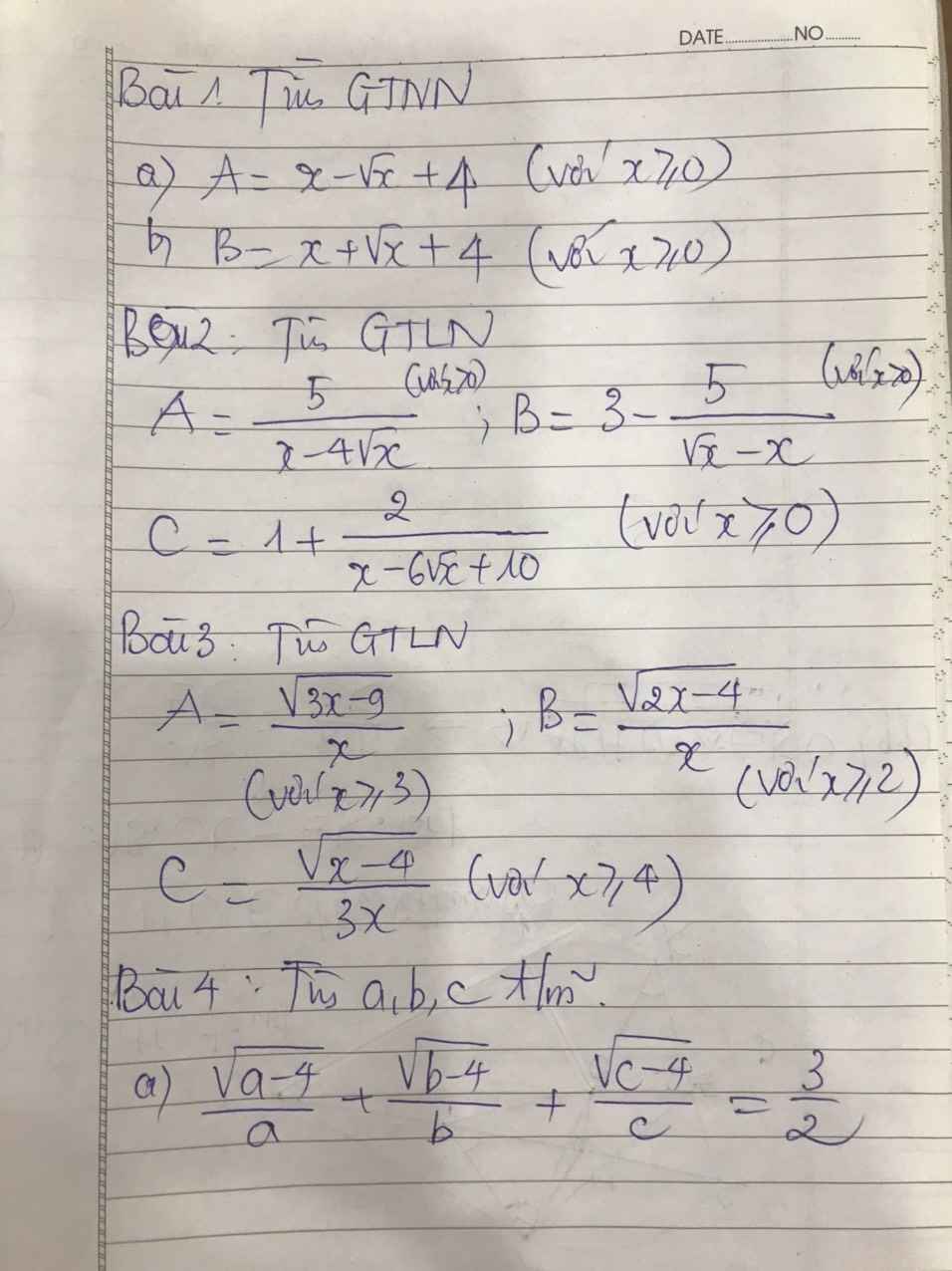
16, \(5\sqrt{3}:\sqrt{15}\)
\(=5\sqrt{3}:\sqrt{5}\cdot\sqrt{3}\)
\(=\dfrac{5\sqrt{3}}{\sqrt{5}\cdot\sqrt{3}}\)
\(=\dfrac{5}{\sqrt{5}}\)
\(=\dfrac{\sqrt{5}\cdot\sqrt{5}}{\sqrt{5}}\)
\(=\sqrt{5}\)
dạ cho mình hỏi s xuống b4 trên tử lại có 2 căn 5 v ạ