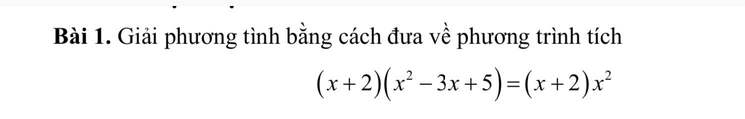K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
P
1
22 tháng 10 2021
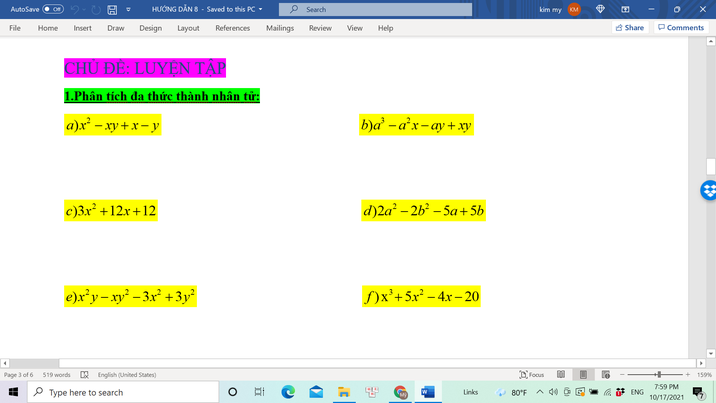
a) \(=x\left(x-y\right)+\left(x-y\right)=\left(x-y\right)\left(x+1\right)\)
b) \(=a^2\left(a-x\right)-y\left(a-x\right)=\left(a-x\right)\left(a^2-y\right)\)
c) \(=3\left(x^2+4x+4\right)=3\left(x+2\right)^2\)
d) \(=2\left(a^2-b^2\right)-5\left(a-b\right)=2\left(a-b\right)\left(a+b\right)-5\left(a-b\right)\)
\(=\left(a-b\right)\left(2a+2b+5\right)\)
e) \(=xy\left(x-y\right)-3\left(x^2-y^2\right)=xy\left(x-y\right)-3\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(xy-3x-3y\right)\)
f) \(=x^2\left(x+5\right)-4\left(x+5\right)=\left(x+5\right)\left(x^2-4\right)\)
\(=\left(x+5\right)\left(x-2\right)\left(x+2\right)\)
NL
2
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
\(3x\left(x-y\right)+x-y\)
\(=3x\left(x-y\right)+1\left(x-y\right)\)
\(=\left(x-y\right)\left(3x+1\right)\)
17 tháng 12 2021
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
QN
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
1
29 tháng 7 2023
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=AC/HA
=>AB*HA=HB*AC
b: AH=căn 5^2-3^2=4cm
BI là phân giác
=>HI/HB=IA/AB
=>HI/3=IA/5=(HI+IA)/(3+5)=0,5
=>HI=1,5cm; IA=1,5cm
23 tháng 12 2021
e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)
21 tháng 7 2021
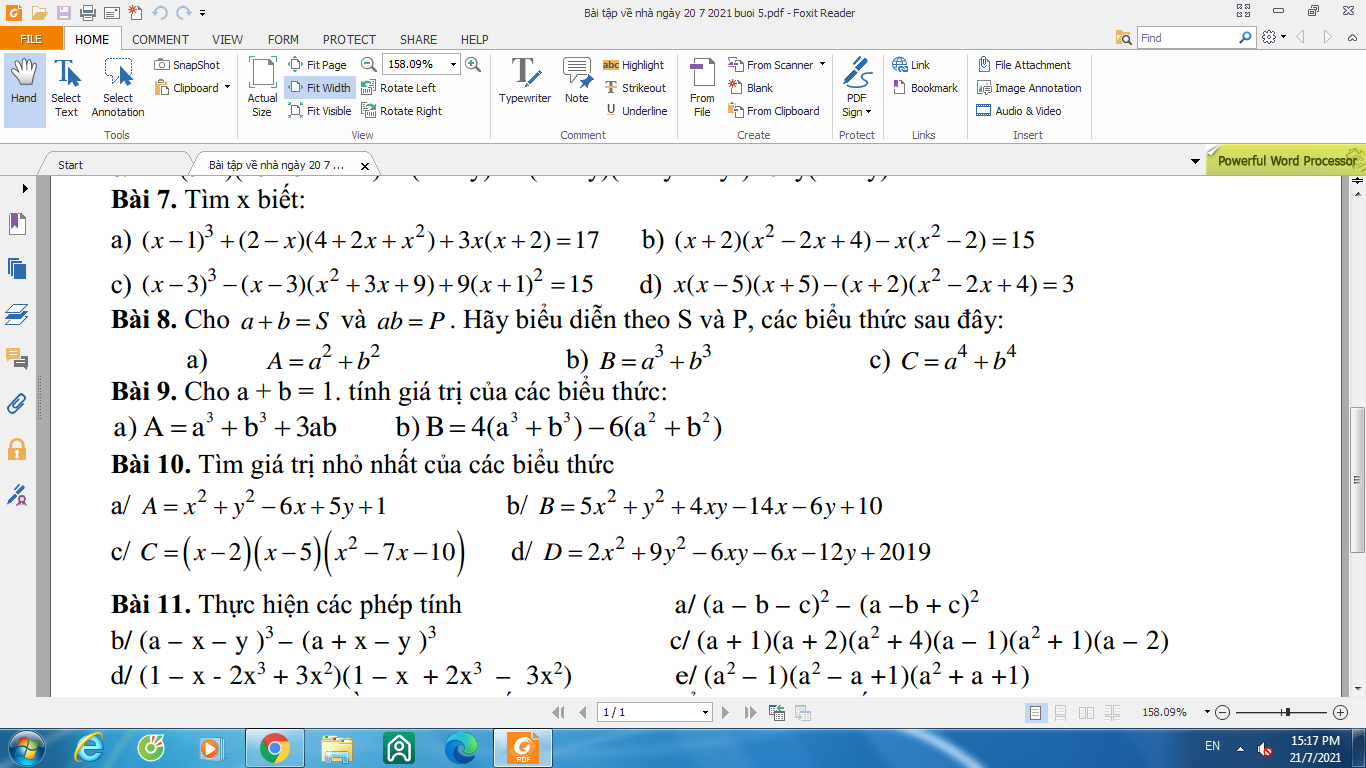
Bài 8
a, \(A=a^2+b^2=\left(a+b\right)^2-2ab\Rightarrow S^2-2P\)
b, \(B=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]\)
\(\Rightarrow S\left(S^2-3P\right)=S^3-3PS\)
c, \(C=a^4+b^4=\left(a^2+b^2\right)^2-2a^2b^2=\left[\left(a+b\right)^2-2ab\right]^2-2\left(ab\right)^2\)
\(\Rightarrow\left(S^2-2P\right)^2-2P^2\)
2 tháng 8 2021
Bài 2:
a) Gọi giao điểm của AC và MD là O
Vì M đối xứng với D qua AC nên AC là đường trung trực của MD
Suy ra: AC vuông góc với MD tại trung điểm của MD
hay O là trung điểm của MD
Xét ΔABC có
M là trung điểm của BC(gt)
MO//AB(cùng vuông góc với AC)
Do đó: O là trung điểm của AC
Xét tứ giác AMCD có
O là trung điểm của đường chéo AC(cmt)
O là trung điểm của đường chéo MD(cmt)
Do đó: AMCD là hình bình hành
mà AC⊥MD
nên AMCD là hình thoi
14 tháng 3 2022
<=> (x+2 ) (x2 - 3x + 5 ) - (x+2 ) x2=0
<=> (x+ 2 ) (x2-3x + 5 - x2) =0
<=> (x + 2 ) (-3x+5)=0
<=> x+2 = 0 hoặc -3x+5=0
x = -2 -3x = -5
x=5/3
NA
21 tháng 3 2022
Áp dụng định lý Ta-lét ta có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\\
\Rightarrow\dfrac{2}{4}=\dfrac{3}{x}\\
\Rightarrow x=3:\dfrac{1}{2}\\
\Rightarrow x=6\left(cm\right)\)