K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 7 2021
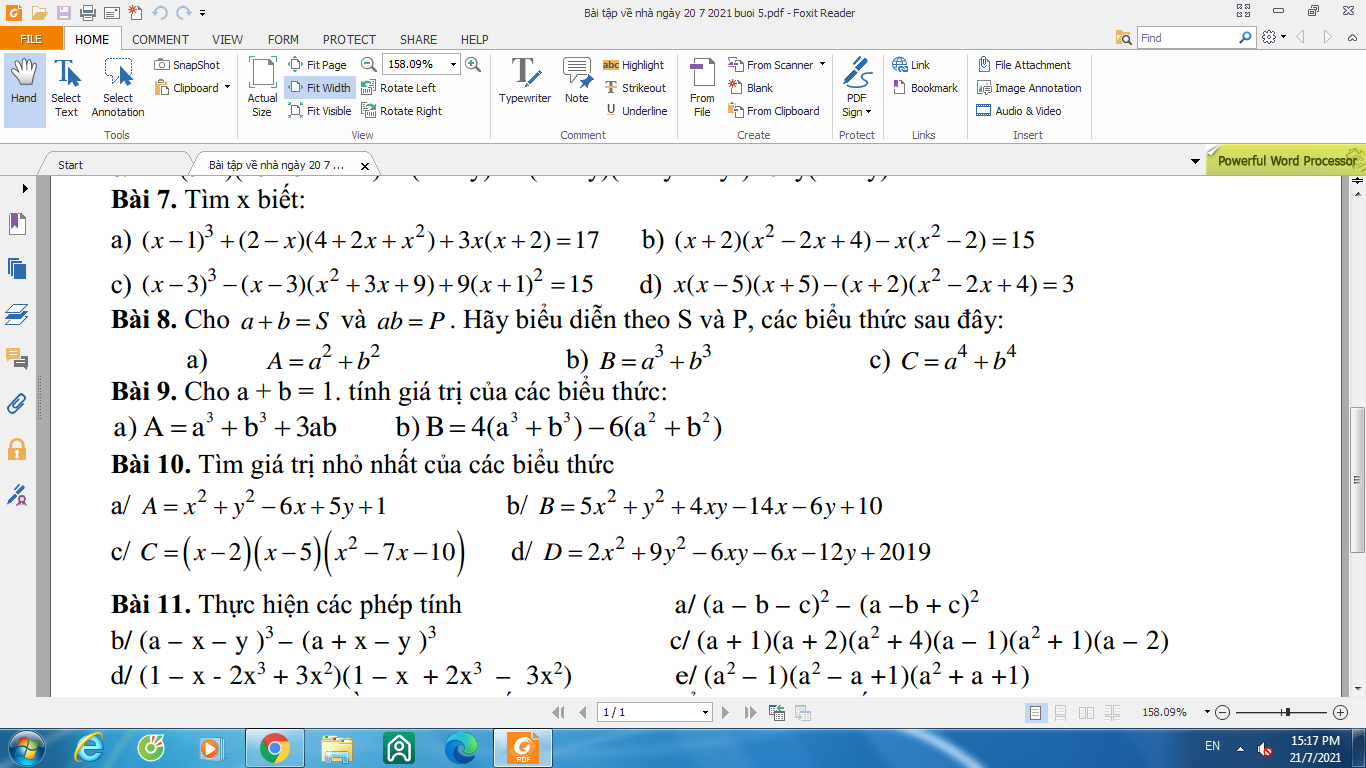
Bài 8
a, \(A=a^2+b^2=\left(a+b\right)^2-2ab\Rightarrow S^2-2P\)
b, \(B=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]\)
\(\Rightarrow S\left(S^2-3P\right)=S^3-3PS\)
c, \(C=a^4+b^4=\left(a^2+b^2\right)^2-2a^2b^2=\left[\left(a+b\right)^2-2ab\right]^2-2\left(ab\right)^2\)
\(\Rightarrow\left(S^2-2P\right)^2-2P^2\)
2 tháng 8 2021
Bài 2:
a) Gọi giao điểm của AC và MD là O
Vì M đối xứng với D qua AC nên AC là đường trung trực của MD
Suy ra: AC vuông góc với MD tại trung điểm của MD
hay O là trung điểm của MD
Xét ΔABC có
M là trung điểm của BC(gt)
MO//AB(cùng vuông góc với AC)
Do đó: O là trung điểm của AC
Xét tứ giác AMCD có
O là trung điểm của đường chéo AC(cmt)
O là trung điểm của đường chéo MD(cmt)
Do đó: AMCD là hình bình hành
mà AC⊥MD
nên AMCD là hình thoi
NA
21 tháng 3 2022
Áp dụng định lý Ta-lét ta có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\\
\Rightarrow\dfrac{2}{4}=\dfrac{3}{x}\\
\Rightarrow x=3:\dfrac{1}{2}\\
\Rightarrow x=6\left(cm\right)\)
11 tháng 1 2022
Bài 1:
b: \(\Leftrightarrow x^2-2x+4+x^3+8=12\)
\(\Leftrightarrow x^3+x^2-2x=0\)
=>x(x+1)=0
=>x=0 hoặc x=-1
f: \(\Leftrightarrow x+3-6x+12=-5\)
=>-5x=-20
hay x=4(nhận)
giúp mik vs mik đag cần gấp
18 tháng 11 2023
a: Xét ΔABC có
AM là đường trung tuyến
G là trọng tâm
Do đó: \(\dfrac{AG}{AM}=\dfrac{2}{3}\)
Xét ΔABM có DG//BM
nên \(\dfrac{AD}{AB}=\dfrac{AG}{AM}\)
=>\(\dfrac{AD}{AB}=\dfrac{2}{3}\)
b: Xét ΔAMC có GE//MC
nên \(\dfrac{AE}{AC}=\dfrac{AG}{AM}\)
=>\(\dfrac{AE}{AC}=\dfrac{2}{3}\)
=>\(AE=\dfrac{2}{3}AC\)
AE+EC=AC
=>\(EC+\dfrac{2}{3}AC=AC\)
=>\(EC=\dfrac{1}{3}AC\)
\(AE=\dfrac{2}{3}AC=2\cdot\dfrac{1}{3}\cdot AC=2\cdot EC\)
VT
0
24 tháng 1
Câu 1:
a: 5x-2=3x+6
=>5x-3x=2+6
=>2x=8
=>\(x=\dfrac{8}{2}=4\)
b: a<=b
=>-2022a>=-2022b
=>-2022a+2021>=-2022b+2021
Câu 2:
1:
a: ĐKXĐ: x<>1
\(\dfrac{3}{x-1}+1=\dfrac{2x+5}{x-1}\)
=>\(\dfrac{3+x-1}{x-1}=\dfrac{2x+5}{x-1}\)
=>\(2x+5=x+2\)
=>x=-3(nhận)
b: |x-9|=2x-3
=>\(\left\{{}\begin{matrix}2x-3>=0\\\left(2x-3\right)^2=\left(x-9\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(2x-3-x+9\right)\left(2x+3+x-9\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(x+6\right)\left(3x-6\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left[{}\begin{matrix}x=-6\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
=>x=2
2:
\(\dfrac{x-3}{2}-\dfrac{3x+2}{4}< \dfrac{1}{3}\)
=>\(\dfrac{6\left(x-3\right)-3\left(3x+2\right)}{12}< \dfrac{4}{12}\)
=>6x-18-9x-6<4
=>-3x-24<4
=>-3x<28
=>\(x>-\dfrac{28}{3}\)
Câu 3:
Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian đi từ A đến B là \(\dfrac{x}{40}\left(giờ\right)\)
Thời gian ô tô đi từ B về A là \(\dfrac{x}{30}\left(giờ\right)\)
Theo đề, ta có phương trình:
\(\dfrac{x}{40}+\dfrac{x}{30}+\dfrac{1}{2}=9+\dfrac{1}{4}\)
=>\(\dfrac{7x}{120}=8,75\)
=>\(x=8,75:\dfrac{7}{120}=120\cdot1,25=150\left(nhận\right)\)
vậy: Độ dài quãng đường AB là 150km