
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Gọi $d$ là ƯCLN của $a$ và $b$. Khi đó:
$a=dx, b=dy$ với $x,y$ là 2 số nguyên tố cùng nhau.
$p=a+b=dx+dy=d(x+y)$.
Hiển nhiên $x+y\geq 2$ nên nếu $d\geq 2$ thì $p=d(x+y)$ không thể là số nguyên tố (trái giả thiết)
Do đó: $d=1$
Tức là $a,b$ nguyên tố cùng nhau. Ta có đpcm.
Bài 2:
** $a,b$ ở đây là các số tự nhiên.
$a^2-b^2=(a-b)(a+b)$. Để $a^2-b^2$ là SNT thì 1 trong 2 thừa số $a-b, a+b$ phải bằng $1$ và số còn lại là SNT.
Mà: $a-b< a+b$ với $a,b\in\mathbb{N}$ nên $a-b=1$
$\Rightarrow a+b=a^2-b^2$

\(\left(2^3\cdot9^4+9^3+45\right):\left(9^2\cdot10-9^2\right)\)
\(=\dfrac{9^3\cdot\left(2^3\cdot9+1\right)+45}{9^3}\)
\(=\dfrac{9^3\cdot73+45}{9^3}=\dfrac{5918}{81}\)


đa thức trên có nghiệm \(\Leftrightarrow x^2-10x=0\)
\(\Leftrightarrow x.\left(x-10\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-10=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x-0\\x=10\end{cases}}}\)
Vậy \(x\in\left\{0;10\right\}\)là nghiệm của đa thức trên

\(B=\frac{3}{51.53}+\frac{3}{53.55}+\frac{3}{55.77}+...+\frac{3}{151.153}\)
\(B=\frac{3}{2}.\left(\frac{1}{51}-\frac{1}{53}+\frac{1}{53}-\frac{1}{55}+\frac{1}{55}-\frac{1}{57}+...+\frac{1}{151}-\frac{1}{153}\right)\)
\(B=\frac{3}{2}.\left(\frac{1}{51}-\frac{1}{153}\right)\)
\(B=\frac{3}{2}.\frac{2}{153}\)
\(B=\frac{1}{51}\)


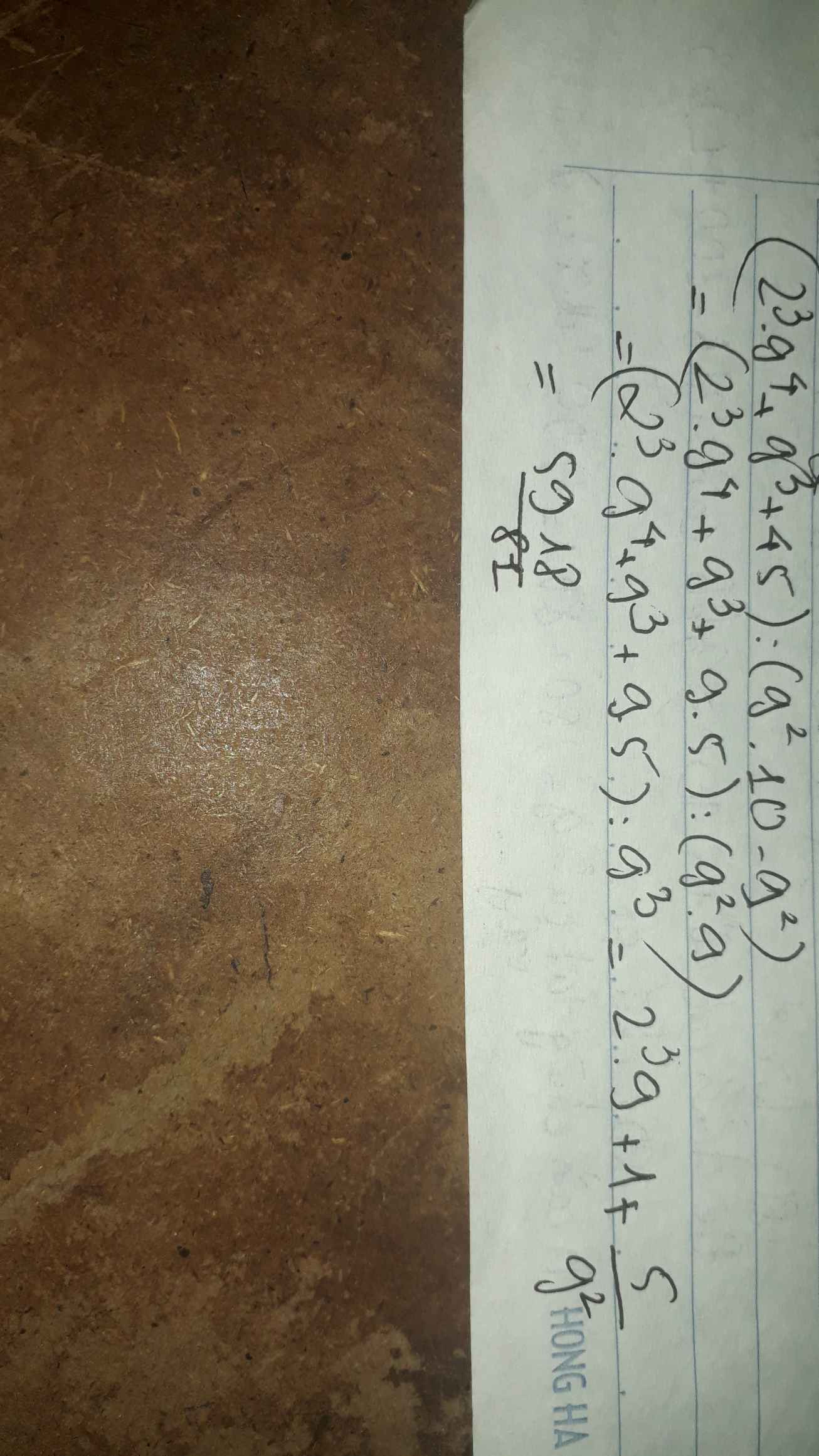
a: Xét ΔADB và ΔKDC có
DA=DK
\(\widehat{ADB}=\widehat{KDC}\)
DB=DC
Do đó: ΔADB=ΔKDC
b: Xét ΔBHD vuông tại H và ΔCID vuông tại I có
DB=DC
\(\widehat{BDH}=\widehat{IDC}\)
Do đó: ΔBHD=ΔCID
Suy ra: DH=DI
=>AH=IK
c: Xét tứ giác BHCI có
BH//CI
BH=CI
Do đó: BHCI là hình bình hành
Suy ra: CH//BI
Cảm ơn bn nhé