
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a, \(\sqrt{\dfrac{\sqrt{5}-2}{\sqrt{5}+2}}+\sqrt{\dfrac{\sqrt{5}+2}{\sqrt{5}-2}}\\ =\sqrt{\dfrac{\left(\sqrt{5}-2\right)^2}{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}}+\sqrt{\dfrac{\left(\sqrt{5}+2\right)^2}{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}+\sqrt{\left(\sqrt{5}+2\right)^2}\)
\(=\sqrt{5}-2+\sqrt{5}+2\\ =2\sqrt{5}\)
b: Ta có: \(\dfrac{2\sqrt{3}-\sqrt{6}}{1-\sqrt{2}}+\dfrac{3}{3-\sqrt{6}}\)
\(=\dfrac{-\sqrt{6}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\dfrac{3\left(3+\sqrt{6}\right)}{3}\)
\(=-\sqrt{6}+3+\sqrt{6}\)
=3

a: Xét (O) có
ΔABK nội tiếp đường tròn
AK là đường kính
Do đó: ΔABK vuông tại B
Xét (O) có
ΔACK nội tiếp đường tròn
AK là đường kính
Do đó: ΔACK vuông tại C
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành

Bài 5:
a) Ta có: \(A=\left(\dfrac{4x+5\sqrt{x}-1}{x\sqrt{x}+2x-\sqrt{x}-2}-\dfrac{3\sqrt{x}+1}{x+\sqrt{x}-2}\right):\dfrac{x+4\sqrt{x}+4}{x-1}\)
\(=\left(\dfrac{4x+5\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(3\sqrt{x}+1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\left(\sqrt{x}+2\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{4x+5\sqrt{x}-1-3x-3\sqrt{x}-\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+2\right)^2}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)^3}\)
\(=\dfrac{\sqrt{x}-1}{x+4\sqrt{x}+4}\)
b) Ta có: \(A-1=\dfrac{\sqrt{x}-1-x-4\sqrt{x}-4}{x+4\sqrt{x}+4}\)
\(=\dfrac{-\left(x+3\sqrt{x}+5\right)}{x+4\sqrt{x}+4}\)
\(=\dfrac{-\left(x+2\cdot\sqrt{x}\cdot\dfrac{3}{2}+\dfrac{9}{4}\right)-\dfrac{11}{4}}{x+4\sqrt{x}+4}< 0\forall x\) thỏa mãn ĐKXĐ
nên A<1

1: Ta có: \(\sqrt{x^2+3x+2}=1\)
\(\Leftrightarrow x^2+3x+2=1\)
\(\Leftrightarrow x^2+3x+1=0\)
\(\text{Δ}=3^2-4\cdot1\cdot1=5\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{5}}{2}\\x_2=\dfrac{-3+\sqrt{5}}{2}\end{matrix}\right.\)

bài 2
a) ĐKXĐ: a\(\ge\)0, a\(\ne\)1
b)P=\(\dfrac{1+\sqrt{a}-1+\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\).\(\dfrac{1+\sqrt{a}}{\sqrt{a}}\)
P=\(\dfrac{2\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}.\dfrac{1+\sqrt{a}}{\sqrt{a}}\)
P=\(\dfrac{2}{1-\sqrt{a}}\)
c) thay a=4 vào biểu thức ta có
P=\(\dfrac{2}{1-\sqrt{4}}\)=\(\dfrac{2}{1-2}\)=-2
d) để P=9 thì
\(\dfrac{2}{1-\sqrt{a}}=9\)\(\Rightarrow\)2=9(1-\(\sqrt{a}\))
\(\Rightarrow\)2=9-\(9\sqrt{a}\)\(\Rightarrow\)\(9\sqrt{a}=7\)\(\Rightarrow\)\(\sqrt{a}=\dfrac{7}{9}\)
\(\Rightarrow a=\dfrac{49}{81}\)
bài 3
a) \(\sqrt{9x^2}=4\Rightarrow3x=4\)\(\Rightarrow\)\(x=\dfrac{4}{3}\)
b)\(\Rightarrow\)\(\left(x-\sqrt{5}\right)^2\)=0\(\Rightarrow x-\sqrt{5}=0\)
\(\Rightarrow x=\sqrt{5}\)

Bài 86:
a: Ta có: \(Q=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
b: Để Q>0 thì \(\sqrt{a}-2>0\)
hay a>4

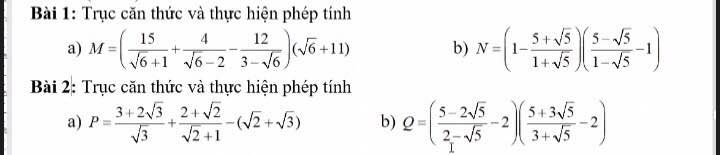



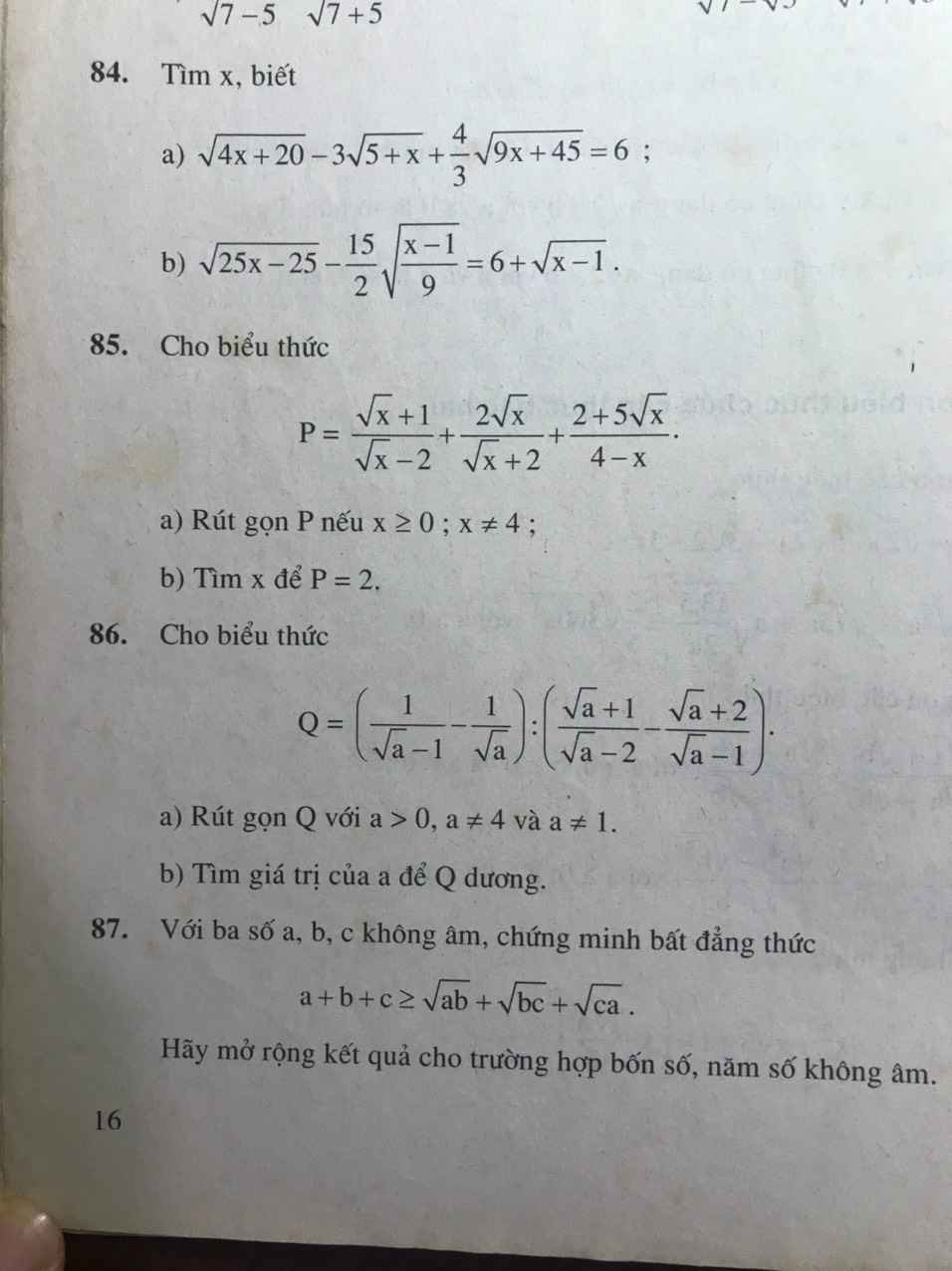
Đáp án : D