giúp mik vs ạ! Cảm ơn mn nhiều!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 9 2021
a: \(x^3+8=\left(x+2\right)\left(x^2-2x+4\right)\)
b: \(27y^3+1=\left(3y+1\right)\left(9y^2-3y+1\right)\)
c: \(x^3-27=\left(x-3\right)\left(x^2+3x+9\right)\)
d: \(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
e: \(8x^3+1=\left(2x+1\right)\left(4x^2-2x+1\right)\)
f: \(27x^3+64y^3=\left(3x+4y\right)\left(9x^2-12xy+16y^2\right)\)
g: \(x^3-\dfrac{1}{8}=\left(x-\dfrac{1}{2}\right)\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)\)
NT
6 tháng 9 2021
c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
KK
6 tháng 9 2021
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)
9 tháng 9 2021
a: Xét ΔADC có
E là trung điểm của AD
K là trung điểm của AC
Do đó: EK là đường trung bình của ΔADC
Suy ra: EK//DC và \(EK=\dfrac{CD}{2}\)
Xét ΔCAB có
K là trung điểm của AC
F là trung điểm của BC
Do đó: KF là đường trung bình của ΔCAB
Suy ra: KF//AB và \(KF=\dfrac{AB}{2}\)
AH
Akai Haruma
Giáo viên
31 tháng 12 2021
Lời giải:
ĐKĐB $\Rightarrow \frac{2}{c}=\frac{a+b}{ab}\Rightarrow c(a+b)=2ab$
Khi đó:
$\frac{a}{b}-\frac{a-c}{c-b}=\frac{a(c-b)-b(a-c)}{b(c-b)}=\frac{ac-ab-ab+bc}{b(c-b)}=\frac{c(a+b)-2ab}{b(c-b)}=\frac{2ab-2ab}{b(c-b)}=0$
$\Rightarrow \frac{a}{b}=\frac{a-c}{c-b}$ (đpcm)
TC
1
13 tháng 7 2023
2:
a: |x-2021|=x-2021
=>x-2021>=0
=>x>=2021
b: 5^x+5^x+2=650
=>5^x+5^x*25=650
=>5^x*26=650
=>5^x=25
=>x=2
c: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{2x+3y-2-6}{2\cdot2+3\cdot3}=2\)
=>x-1=4 và y-2=6
=>x=5 và y=8
5:
a: Xét tứ giác ABKC có
M là trung điểm chung của AK và BC
=>ABKC là hình bình hành
=>góc ABK=180 độ-góc CAB=80 độ
b: ABKC là hình bình hành
=>góc ABK=góc ACK
góc DAE=360 độ-góc CAB-góc BAD-góc CAE
=180 độ-góc CAB=góc ACK
Xét ΔABK và ΔDAE có
AB=DA
góc ABK=góc DAE
BK=AE
=>ΔABK=ΔDAE
25 tháng 9 2021
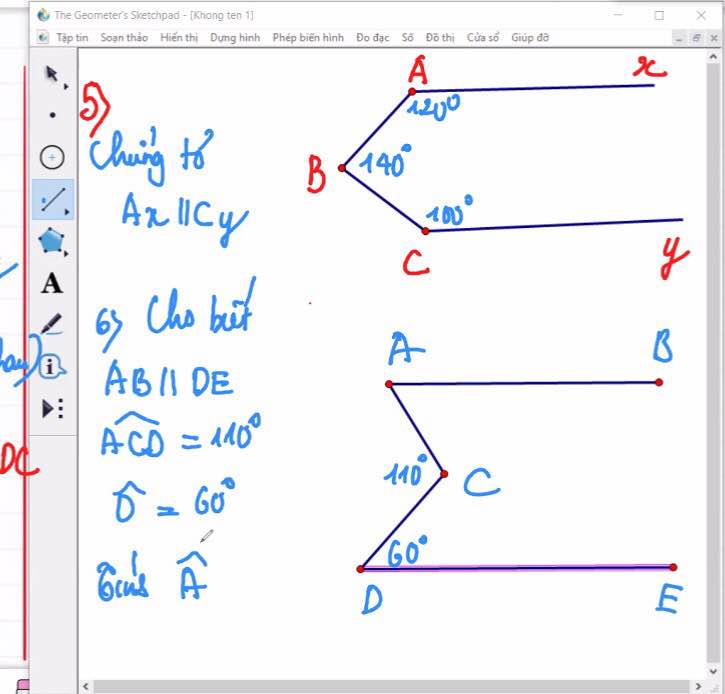
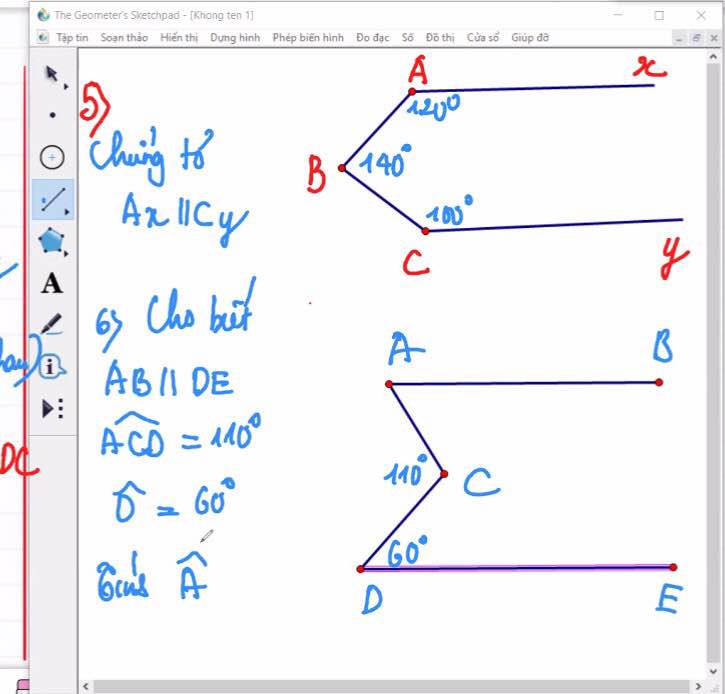
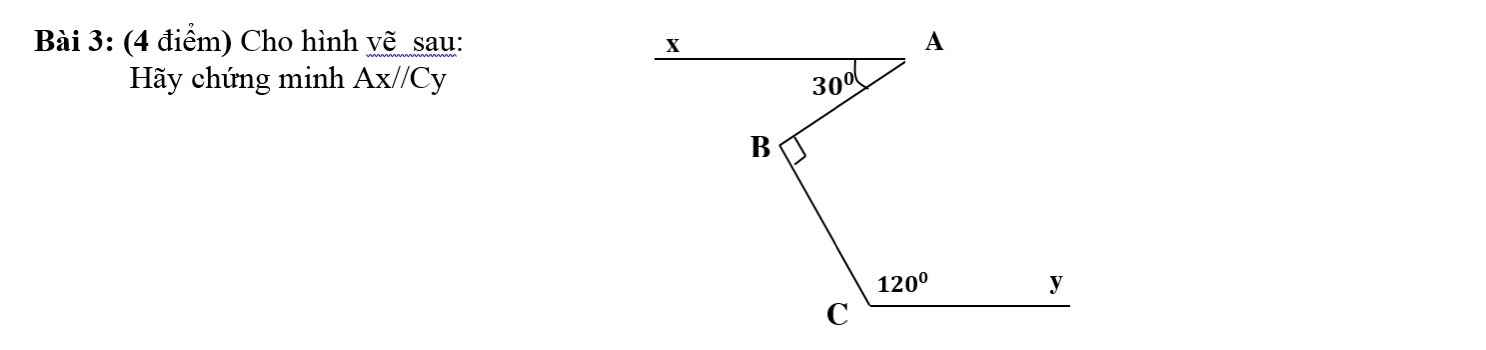
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy
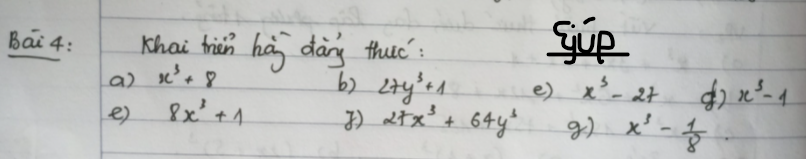
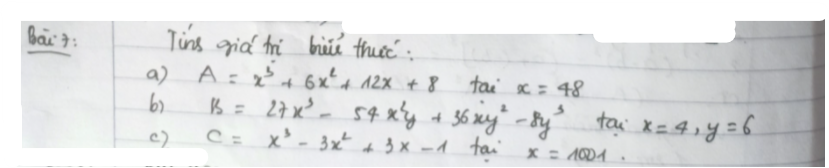
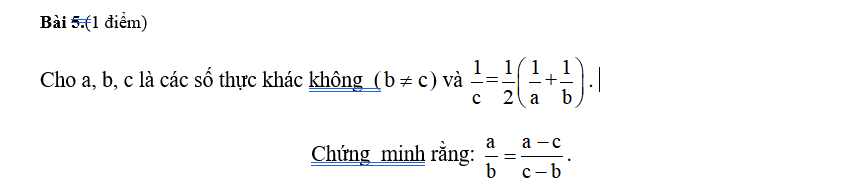
c) 4 . \(\frac{1^2}{4^2}\)+ 25 . (\(\frac{3}{4}\): \(\frac{5}{4}\))3: \(\frac{3^3}{2^3}\)3
4 . \(\frac{1}{16}\)+ 25 . ( \(\frac{3}{4}\). \(\frac{4}{5}\)) 3: \(\frac{27}{8}\)
\(\frac{1}{4}\)+ 25 . ( \(\frac{3}{5}\)) 3. \(\frac{8}{27}\)
\(\frac{1}{4}\)+ 25 .\(\frac{3^3}{5^3}\). \(\frac{8}{27}\)
\(\frac{1}{4}\)+25 . \(\frac{27}{125}\) . \(\frac{8}{27}\)
\(\frac{1}{4}\)+25 . \(\frac{8}{125}\)
\(\frac{1}{4}\)+\(\frac{8}{5}\)
\(\frac{5}{20}\)+ \(\frac{32}{20}\)
\(\frac{37}{20}\)
Bạn tự bổ sung dấu = vào nhé