K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Giup mik voi
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2021
\(12x^5y^7:3xy^7=4x^4\)
\(\left(2x^3-x^2+5x\right):x=2x^2-x+5\)
giup mik voi :(
11 tháng 5 2022
-Áp dụng BĐT AM-GM cho 2 số dương ta có:
\(xy+1\ge2\sqrt{xy.1}=2\sqrt{xy}\)
\(\Rightarrow y\ge xy+1\ge2\sqrt{xy}\)
\(\Rightarrow\sqrt{y}\ge2\sqrt{x}\)
\(\Rightarrow\sqrt{\dfrac{y}{x}}\ge2\)
\(\Rightarrow\dfrac{y}{x}\ge4\)
\(\Rightarrow\dfrac{x}{y}\le\dfrac{1}{4}\left(đpcm\right)\)
-Dấu "=" xảy ra khi \(x=\dfrac{1}{2};y=2\)
6 tháng 10 2021
1: Ta có: \(3\left(x+5\right)-2\left(4-3x\right)=7\)
\(\Leftrightarrow3x+15-8+6x=7\)
\(\Leftrightarrow9x=14\)
hay \(x=\dfrac{14}{9}\)
2: Ta có: \(x\left(7-2x\right)+2x\left(x-2\right)=15\)
\(\Leftrightarrow7x-2x^2+2x^2-4x=15\)
\(\Leftrightarrow3x=15\)
hay x=5
3: Ta có: \(2x\left(9x-4\right)-9x\left(2x-3\right)=-38\)
\(\Leftrightarrow18x^2-8x-18x^2+27x=-38\)
\(\Leftrightarrow19x=-38\)
hay x=-2
6 tháng 10 2021
7: Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x-5\right)^2=30\)
\(\Leftrightarrow x^2-5-x^2+10x-25=30\)
\(\Leftrightarrow10x=60\)
hay x=6
8: Ta có: \(\left(x+2\right)\left(x-2\right)+8=\left(x-1\right)^2\)
\(\Leftrightarrow x^2-4+8=x^2-2x+1\)
\(\Leftrightarrow-2x=3\)
hay \(x=-\dfrac{3}{2}\)
VT
5
22 tháng 8 2021
\(\left(3x-2\right)\left(5x+4\right)-\left(2x+7\right)\left(4x-1\right)+1\)
\(=15x^2+2x-8-8x^2-26x+7+1=7x^2-24x\)
20 tháng 10 2021
\(25a^2-25x^2+10x-1\)
\(=25a^2-\left(5x-1\right)^2\)
\(=\left(5a-5x+1\right)\left(5a+5x-1\right)\)
30 tháng 6 2020
Bài này dễ thôi bạn.
Trả lời:
3x - 7 = 5
3x = 5 + 7
3x = 12
x = 12:3
x = 4
Vậy x = 4
Ủng hộ nhé
9 tháng 3 2020
<=> x3 - 4x2 - x + 4 = 0
<=> (x2 - 1)(x - 4) = 0
<=> (x - 1)(x + 1)(x - 4) = 0
<=> x = 1 hoặc x = -1 hoặc x = 4
9 tháng 3 2020
\(x^3-4x^2+4-x=0\)
\(\left(x-1\right)\left(x-4\right)\left(x+1\right)=0\)
\(x=\pm1;x=4\)
sắp tới lập nhóm nha :v ( quảng cáo lun )
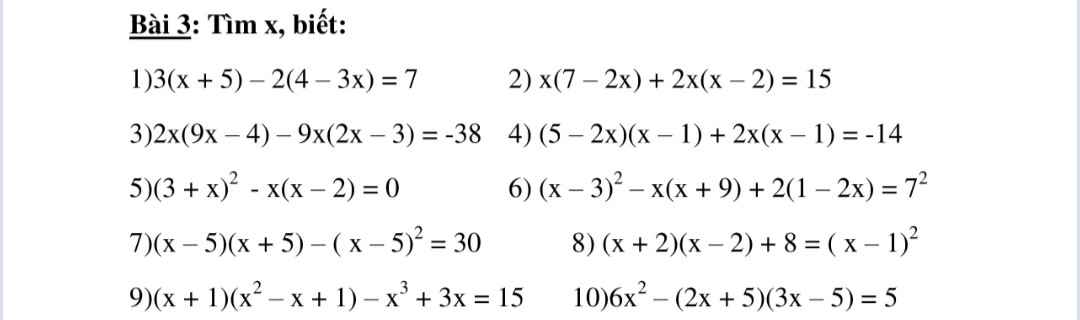
a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB~ΔOCD
b: Sửa đề: cắt BC tại N
Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)
=>\(OM\cdot AC=DC\cdot AO\)
c: Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)(1)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BO}{BD}\left(2\right)\)
Ta có: ΔOAB~ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra OM=ON
=>O là trung điểm của MN