
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hàm số bậc nhất y = a x + b xác định với mọi giá trị của x thuộc R và có tính chất sau:
- Đồng biến trên R nếu a > 0
- Nghịch biến trên R nếu a < 0
Đáp án cần chọn là: C

Đáp án C
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của thuộc R và có tính chất sau:
• Đồng biến trên R nếu a > 0
• Nghịch biến trên R nếu a < 0

Đáp án C
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của thuộc R và có tính chất sau:
• Đồng biến trên R nếu a > 0
• Nghịch biến trên R nếu a < 0

Câu 2: \(\sqrt{x-2}=2\left(ĐKXĐ:x>=2\right)\)
=>x-2=4
=>x=6(nhận)
=>x2=62=36
=>Chọn D
Câu 4:
\(\sqrt{a+b-9}+\sqrt{a+b+1}\)
\(=\dfrac{\left(a+b-9\right)-\left(a+b+1\right)}{\sqrt{a+b-9}-\sqrt{a+b+1}}\)
\(=\dfrac{-10}{-2}=5\)
=>Chọn D

Xét ta giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức :
\(AB^2=BH.BC=BH.\left(CH+BH\right)\Rightarrow25=BH\left(\frac{144}{13}+BH\right)\Rightarrow BH=\frac{25}{13}\)cm
\(\Rightarrow BC=HB+HC=\frac{144}{13}+\frac{25}{13}=\frac{196}{13}\)
* Áp dụng hệ thức : \(AC^2=HC.BC=\frac{144}{13}.\frac{169}{13}=144\Rightarrow AC=12\)cm

a) Ta có: \(\sqrt{\dfrac{a}{b}}+\sqrt{ab}+\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}\)
\(=\dfrac{\sqrt{ab}}{b}+\sqrt{ab}+\dfrac{a}{b}\cdot\dfrac{\sqrt{b}}{\sqrt{a}}\)
\(=\dfrac{\sqrt{ab}}{b}+\dfrac{b\sqrt{ab}}{b}+\dfrac{\sqrt{ab}}{b}\)
\(=\dfrac{b\sqrt{ab}+2\sqrt{ab}}{b}\)
b) \(\sqrt{\dfrac{m}{x^2-2x+1}}\cdot\sqrt{\dfrac{4mx^2-8mx+4m}{81}}\)
\(=\sqrt{\dfrac{m}{\left(x-1\right)^2}\cdot\dfrac{4m\left(x-1\right)^2}{81}}\)
\(=\sqrt{\dfrac{4m^2}{81}}=\dfrac{2m}{9}\)












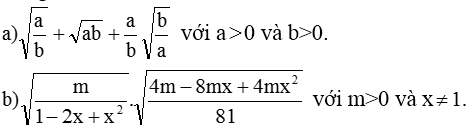
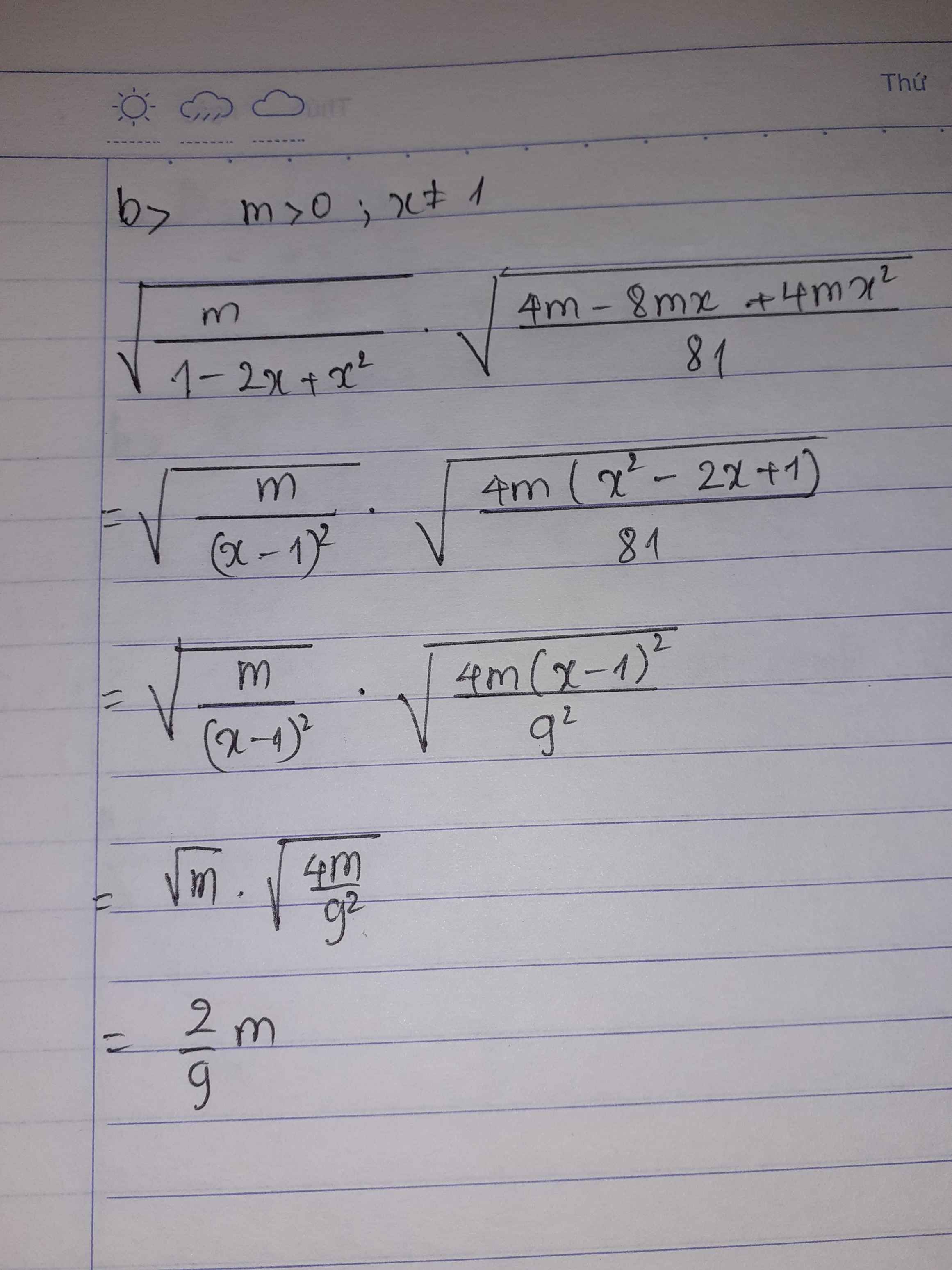
Câu b:
Lượng điện tiêu thụ trong tháng 5 của nhà anh Thành là:
31 x (4 x 18 x 4+ 100 x 8 + 3 x 900 + 1040 + 48 x 10 x 2)= 179 428 (W.h)= 179,428(kW.h)
Tiền điện anh Thành phải trả:
50 x 1678 + 50 x 1734 + 79,428 x 2014= 330567,992 (đồng)= 330 568 đồng