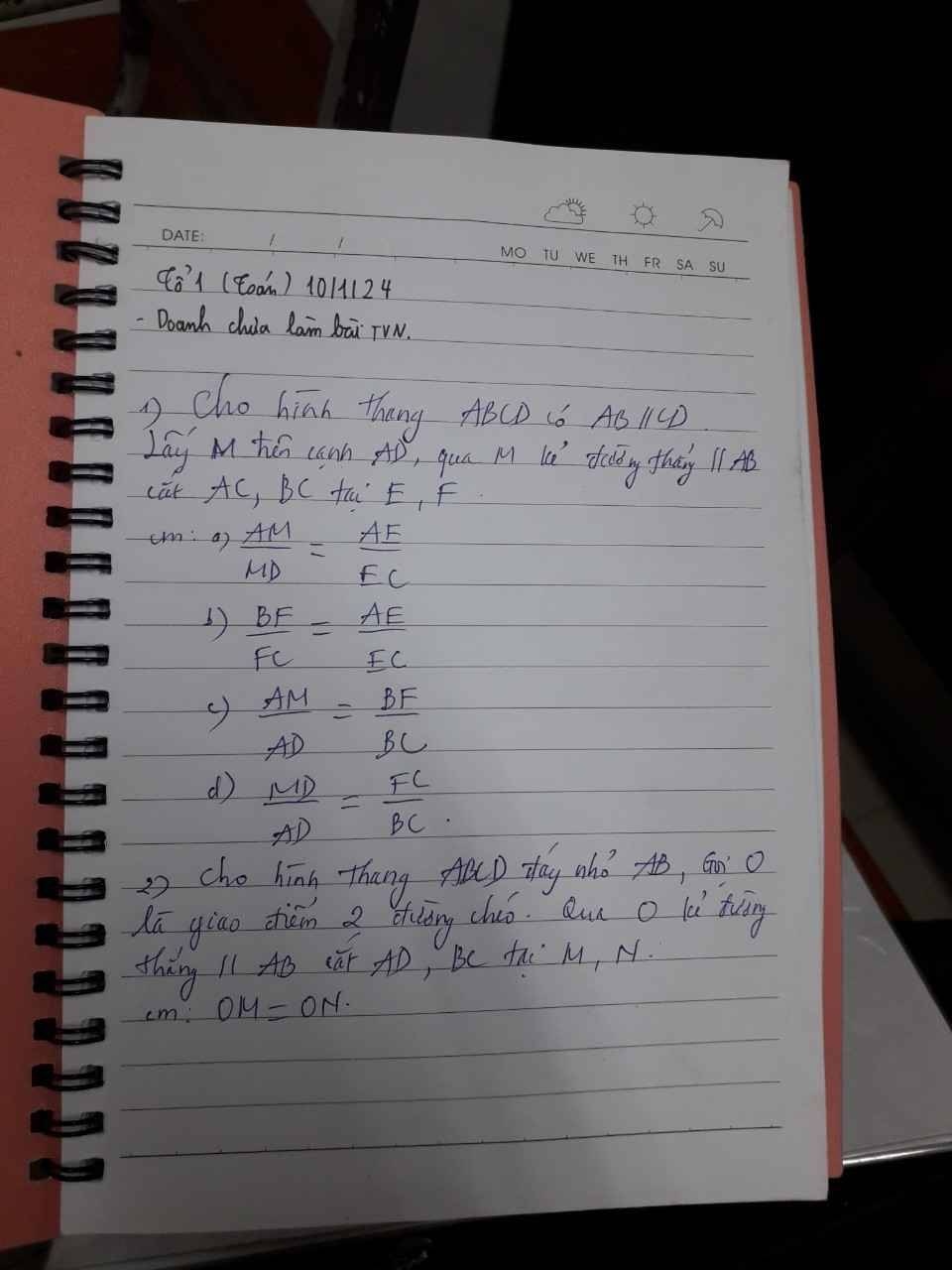Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(2)\left(x-1\right)-\left(2x-1\right)=9-x.\\ \Leftrightarrow x-1-2x+1-9+x=0.\\ \Leftrightarrow0x-9=0. \)
\(\Leftrightarrow0x=9\) (vô lý).
\(3)x\left(x+3\right)^2-3x=\left(x+2\right)^3+1.\\ \Leftrightarrow x\left(x^2+6x+9\right)-3x=x^3+6x^2+12x+8+1.\\ \Leftrightarrow x^3+6x^2+9x-3x-x^3-6x^2-12x-9=0.\\ \Leftrightarrow-6x=9.\\ \Leftrightarrow x=\dfrac{-3}{2}.\)

2: 3-x<0
=>-x<-3
=>x>3
=>x=4
3: AH=căn 1*4=2cm
S ABC=1/2*2*5=5cm2

Câu 1:
a.
$x+y=\frac{1-\sqrt{5}+1+\sqrt{5}}{2}=1$
$xy=\frac{(1-\sqrt{5})(1+\sqrt{5})}{2}=-1$
$x^2+y^2=(x+y)^2-2xy=1-2(-1)=3$
Khi đó:
$S=\frac{1}{(x-1)^2}+\frac{1}{(y-1)^2}=\frac{1}{(-y)^2}+\frac{1}{(-x)^2}=\frac{1}{x^2}+\frac{1}{y^2}$
$=\frac{x^2+y^2}{(xy)^2}=\frac{3}{(-1)^2}=3$
b.
Vì $x+y+z=0$ nên $x+y=-z$
$\Rightarrow x^2+y^2+2xy=z^2$
$\Rightarrow x^2+y^2-z^2=-2xy$
Tương tự với các phân thức còn lại ta có:
\(\sum \frac{1}{x^2+y^2-z^2}=\frac{1}{-2xy}+\frac{1}{-2yz}+\frac{1}{-2zx}=\frac{x+y+z}{-2xyz}=\frac{0}{-2xyz}=0\)
Ta có đpcm.

Ta có \(x.\left(x^2+x+1\right)-x^2.\left(1+x\right)-x-7\)
\(=x^3+x^2+x-x^2-x^3-x-7\)
\(=\left(x^3-x^3\right)-\left(x^2-x^2\right)-\left(x-x\right)-7\)
\(=-7\)
Do đó giá trị của biểu thức không phụ thuộc vào biến
Vậy...

a. -2x(x3 - 3x2 - x + 1)
= -2x4 + 6x3 + 2x2 - 2x
c. 3x2(2x3 - x + 5)
= 6x5 - 3x3 + 15x2
Bài 3:
a: Ta có: \(6x\left(5x-3\right)+3x\left(1-10x\right)=7\)
\(\Leftrightarrow30x^2-18x+3x-30x^2=7\)
\(\Leftrightarrow x=-\dfrac{7}{15}\)
b: Ta có: \(3x\left(12x-4\right)-9x\left(4x-3\right)=30\)
\(\Leftrightarrow36x^2-12x-36x^2+27x=30\)
hay x=2
c: ta có: \(x\left(5-2x\right)-2x\cdot\left(x-1\right)=15\)
\(\Leftrightarrow5x-2x^2-2x^2+2x-15=0\)
\(\Leftrightarrow-4x^2+7x-15=0\)
\(\text{Δ}=7^2-4\cdot\left(-4\right)\cdot\left(-15\right)=-191\)
Vì Δ<0 nên phương trình vô nghiệm

Câu 1:
a: Xét ΔADC có ME//DC
nên \(\dfrac{AM}{MD}=\dfrac{AE}{EC}\)
b: Xét ΔCAB có EF//AB
nên \(\dfrac{CE}{EA}=\dfrac{CF}{FB}\)
=>\(\dfrac{AE}{EC}=\dfrac{BF}{FC}\)
c: ta có: \(\dfrac{AM}{MD}=\dfrac{AE}{EC}\)
\(\dfrac{AE}{EC}=\dfrac{BF}{FC}\)
Do đó: \(\dfrac{AM}{MD}=\dfrac{BF}{FC}\)
d: Ta có: \(\dfrac{AM}{MD}=\dfrac{BF}{FC}\)
=>\(\dfrac{AM+MD}{MD}=\dfrac{BF+FC}{FC}\)
=>\(\dfrac{AD}{MD}=\dfrac{BC}{FC}\)
=>\(\dfrac{DM}{DA}=\dfrac{CF}{CB}\)
Bài 2:
Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AM}{AD}\)(1)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BN}{BC}\left(2\right)\)
Xét hình thang ABCD có MN//AB//CD
nên \(\dfrac{AM}{MD}=\dfrac{BN}{NC}\)
=>\(\dfrac{MD}{AM}=\dfrac{CN}{BN}\)
=>\(\dfrac{MD+AM}{AM}=\dfrac{CN+BN}{BN}\)
=>\(\dfrac{AD}{AM}=\dfrac{BC}{BN}\)
=>\(\dfrac{AM}{AD}=\dfrac{BN}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra OM=ON

1: Sửa đề: Qua N kẻ đường song song với PC cắt AB tại F
Xét tứ giác CNFP có NF//PC
nên CNFP là hình thang