K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 9 2021
Xét ΔIDK vuông tại D và ΔIDC vuông tại D có
ID chung
DK=DC
Do đó: ΔIDK=ΔIDC
Suy ra: \(\widehat{KID}=\widehat{DIC}\)
mà \(\widehat{KID}=\widehat{AIB}\)
nên \(\widehat{AIB}=\widehat{DIC}\)
5 tháng 8 2023
m: \(=x^m\cdot x^2-x^m=x^m\left(x^2-1\right)=x^m\left(x-1\right)\left(x+1\right)\)
n: \(=5\cdot x^m\cdot x^2+10x^2\)
\(=5x^2\left(x^m+2\right)\)
o: \(=5x\left(x-2y\right)+2\left(x-2y\right)^2\)
\(=\left(x-2y\right)\left(5x+2x-4y\right)\)
=(x-2y)(7x-4y)
p: \(=7x\left(y-4\right)^2+\left(y-4\right)^3\)
\(=\left(y-4\right)^2\cdot\left(7x+y-4\right)\)
q: \(\left(4x-8\right)\left(x^2+6\right)-\left(4x-8\right)\left(x+7\right)+9\left(8-4x\right)\)
\(=\left(4x-8\right)\left(x^2+6-x-7\right)-9\left(4x-8\right)\)
\(=\left(4x-8\right)\left(x^2-x-10\right)\)
\(=4\left(x-2\right)\left(x^2-x-10\right)\)
H9
HT.Phong (9A5)
CTVHS
5 tháng 8 2023
m) \(x^{m+2}-x^m\)
\(=x^m\cdot x^2-x^m\)
\(=x^m\left(x^2-1\right)\)
\(=x^m\left(x^2-1^2\right)\)
\(=x^m\left(x-1\right)\left(x+1\right)\)
n) \(5x^{m+2}+10x^2\)
\(=5x^m\cdot x^2+10x^2\)
\(=5x^2\cdot x^m+10x^2\)
\(=5x^2\left(x^m+2\right)\)
o) \(5x\left(x-2y\right)+2\left(2y-x\right)^2\)
\(=5x\left(x-2y\right)+2\left(x-2y\right)^2\)
\(=\left(x-2y\right)\left[5x+2\left(x-2y\right)\right]\)
\(=\left(x-2y\right)\left(5x+2x-4y\right)\)
\(=\left(x-2y\right)\left(7x-4y\right)\)
p) \(7x\left(y-4\right)^2-\left(4-y\right)^3\)
\(=7x\left(4-y\right)^2-\left(4-y\right)^3\)
\(=\left(4-y\right)^2\left[7x-\left(4-y\right)\right]\)
\(=\left(4-y\right)^2\left(7x-4+y\right)\)
q) \(\left(4x-8\right)\left(x^2+6\right)-\left(4x-8\right)\left(x+7\right)+9\left(8-4x\right)\)
\(=4\left(x-2\right)\left(x^2+6\right)-4\left(x-2\right)\left(x+7\right)-36\left(x-2\right)\)
\(=4\left(x-2\right)\left[\left(x^2+6\right)-\left(x+7\right)-9\right]\)
\(=4\left(x-2\right)\left(x^2+6-x-7-9\right)\)
\(=4\left(x-2\right)\left(x^2-x-10\right)\)
NP
2
7 tháng 4 2021
Ta có: 3(x-2)=2x-9
\(\Leftrightarrow3x-6-2x+9=0\)
\(\Leftrightarrow x=-3\)
Để (1) và (2) tương đương thì \(-3\left(m-3\right)=m+1\)
\(\Leftrightarrow-3m+9-m-1=0\)
\(\Leftrightarrow-4m=-8\)
hay m=2
Vậy: Để hai phương trình tương đương thì m=2
7 tháng 4 2021
Ta có: 3(x-2)=2x-9
⇔3x−6−2x+9=0⇔3x−6−2x+9=0
⇔x=−3⇔x=−3
Để (1) và (2) tương đương thì −3(m−3)=m+1−3(m−3)=m+1
⇔−3m+9−m−1=0⇔−3m+9−m−1=0
⇔−4m=−8⇔−4m=−8
hay m=2
Vậy: Để hai phương trình tương đương thì m=2
19 tháng 6 2023
a: CH=16^2/24=256/24=32/3(cm)
BC=24+32/3=104/3cm
AC=căn 32/3*104/3=16/3*căn 13(cm)
b: BC=12^2/6=144/6=24cm
CH=24-6=18cm
AC=căn 18*24=12*căn 3(cm)
15 tháng 1 2022
Để phương trình trên là phương trình bậc nhất 1 ẩn thì
\(\left(2m+3\right)\left(1-m\right)\left(x-m\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2m+3=0\\1-m=0\\x-m=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=1\\m=x\end{matrix}\right.\)
23 tháng 12 2021
e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)
7 tháng 3 2021
Với m = 1 hoặc m = -1 ta có:
0x = m
\(\Rightarrow\) m = 0
Với m \(\ne\) \(\pm1\) ta có:
x = \(\dfrac{m}{m^2-1}=\dfrac{m}{\left(m+1\right)\left(m-1\right)}\)
Vậy ...
Chúc bn học tốt! (Chắc vậy!)
NL
2
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
\(3x\left(x-y\right)+x-y\)
\(=3x\left(x-y\right)+1\left(x-y\right)\)
\(=\left(x-y\right)\left(3x+1\right)\)
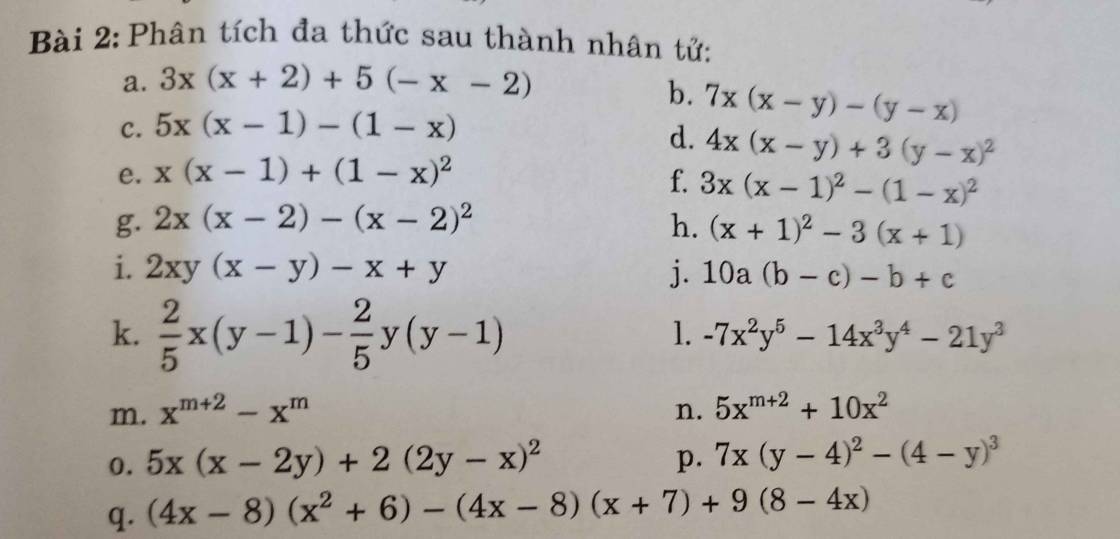
Xet ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=OB/OD
=>CE/DE=DF/CF
=>\(\dfrac{CF+FE}{DE}=\dfrac{DE+EF}{CF}\)
=>\(CF^2+FE\cdot CF=DE^2+DE\cdot FE\)
=>(CF-DE)(CF+DE)-FE(CF-DE)=0
=>(CF-DE)(CF+DE-FE)=0
=>CF=DE