K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
0
10 tháng 9 2023
a) \(x^2+xy+y^2+1\)
\(=x^2+xy+\dfrac{y^2}{4}-\dfrac{y^2}{4}+y^2+1\)
\(=\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1\)
mà \(\left\{{}\begin{matrix}\left(x+\dfrac{y}{2}\right)^2\ge0,\forall x;y\\\dfrac{3y^2}{4}\ge0,\forall x;y\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1>0,\forall x;y\)
\(\Rightarrow dpcm\)
10 tháng 9 2023
b) \(...=x^2-2x+1+4\left(y^2+2y+1\right)+z^2-6z+9+1\)
\(=\left(x-1\right)^2+4\left(y^{ }+1\right)^2+\left(z-3\right)^2+1>0,\forall x.y\)
\(\Rightarrow dpcm\)
30 tháng 9 2021
\(A=\dfrac{x^3\left(x+1\right)+\left(x+1\right)}{x^2\left(x+1\right)-\left(x+1\right)}=\dfrac{\left(x^3+1\right)\left(x+1\right)}{\left(x^2-1\right)\left(x+1\right)}\)
\(=\dfrac{x^3+1}{x^2-1}=\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{x^2-x+1}{x-1}\)
AH
Akai Haruma
Giáo viên
1 tháng 10 2021
Lời giải:
b.
$B=\frac{x^3-3x^2y+3xy^2-y^3-3x^2y-3xy^2+y^3}{x-6y}$
$=\frac{x^3-6x^2y}{x-6y}=\frac{x^2(x-6y)}{x-6y}=x^2$
c.
$C=\frac{(3x-1)(x-1)^2}{(2x+3)(x-1)^2}=\frac{3x-1}{2x+3}$
d.
$D=\frac{(x+3)(x-1)-(2x-1)(x+1)}{(x+1)(x-1)}-\frac{x-3}{(x-1)(x+1)}$
$=\frac{-x^2+1}{(x-1)(x+1)}=\frac{-(x^2-1)}{x^2-1}=-1$
23 tháng 10 2021
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2021
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
KV
21 tháng 10 2023
a) Thể tích không khí bên trong lều:
2².2 : 3 = 8/3 (m³)
b) Số vải bạt cần dùng:
2² + 4.2.2,24 : 2 = 4 + 8,96 = 12,96 (m²)
26 tháng 7 2023
6:
a: Xét ΔCDM và ΔBAM có
MC=MB
góc CMD=góc BMA
MD=MA
=>ΔCDM=ΔBAM
b: ΔCDM=ΔBAM
=>góc CDM=góc BAM
=>CD//AB
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC//BD và AC=BD và AB=DC
c: Xét ΔABC có AB>AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB>HC
Xét ΔECB có HB>HC
mà HB,HC lần lượt là hình chiếu của EB,EC trên BC
nên EB>EC
21 tháng 10 2021
Bài 4:
\(A=2x^2+3x-10x-15-2x^2+6x+x+7=-8\\ B=x^3-y^3-5+2y^3-x^3-y^3=-5\\ C=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6x^2+6=4\)
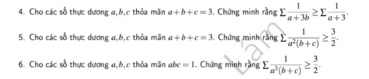
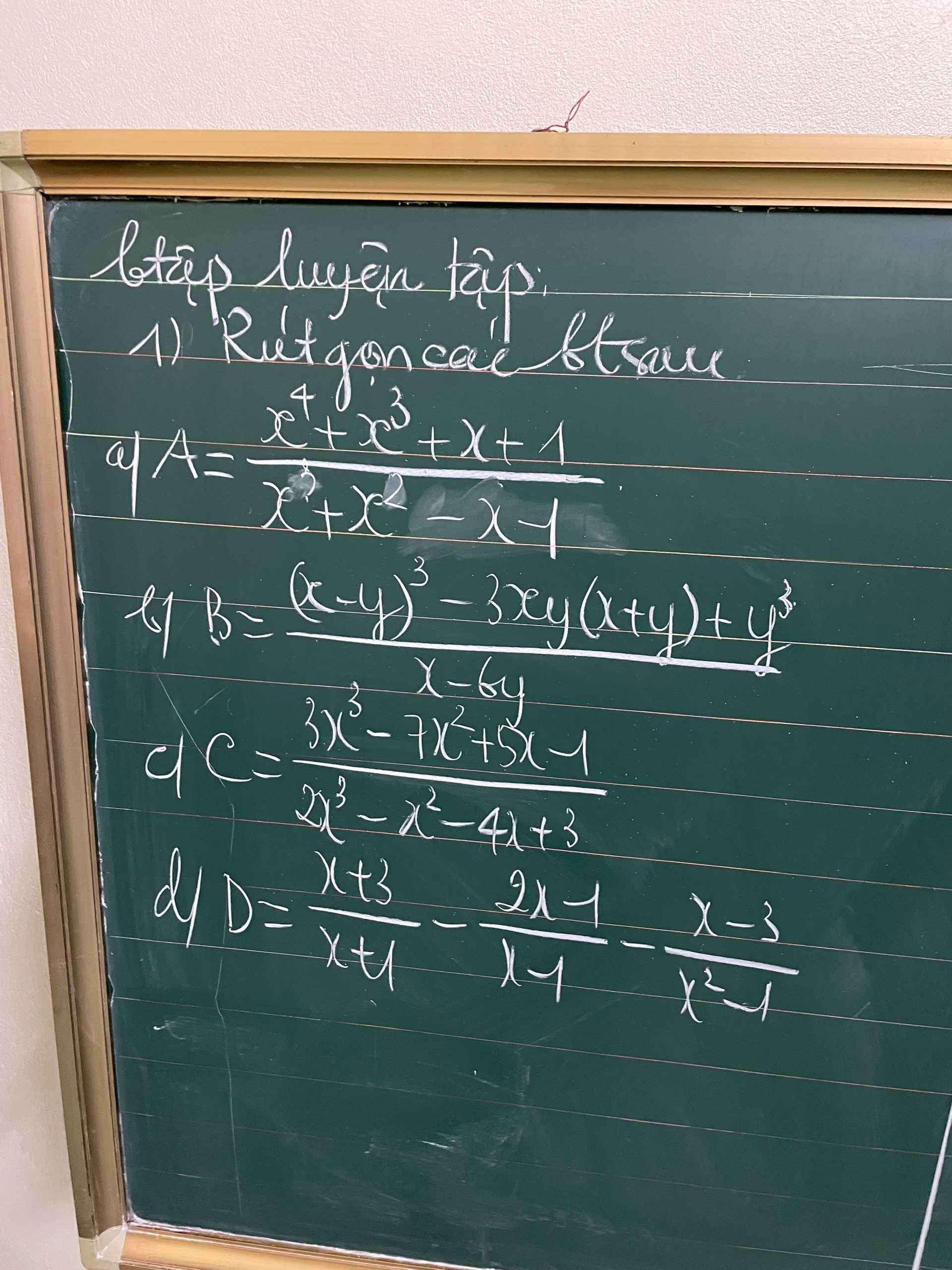
đề bài dou e
giúp j vậy bn?