
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\sqrt{9x+3}=6\)
\(\Leftrightarrow9x+3=36\)
hay x=11/3

Coi hình là tam giác $ABC$ vuông tại $A$, đường cao $AH$ và $AC=8$ cm
Câu 71:
Áp dụng HTL trong tam giác vuông:
$8^2=(10-x).10$
$\Leftrightarrow 10x=36$
$\Leftrightarrow x=3,6$ (cm)
Đáp án B
Câu 72:
Theo kết quả bài 71 thì $BH=3,6$ (cm)
$CH=BC-BH=10-3,6=6,4$ (cm)
Áp dụng htl trong tgv:
$x=AH=\sqrt{BH.CH}=\sqrt{6,4.3,6}=4, 8$ (cm)
Đáp án A.
Câu 73:
Áp dụng định lý Pitago:
$CH=\sqrt{AC^2-AH^2}=\sqrt{5^2-3^2}=4$
Áp dụng HTL trong tam giác vuông:
$BH=\frac{AH^2}{CH}=\frac{3^2}{4}=2,25$
$x=BC=BH+CH=2,25+4=6,25$
Đáp án D

\(b,\text{PT hoành độ giao điểm: }-x-7=-3x+1\Leftrightarrow x=4\Leftrightarrow y=-11\Leftrightarrow B\left(4;-11\right)\\ c,\text{Gọi }\left(D_3\right):y=ax+b\left(a\ne0\right)\\ \left(D_3\right)\text{//}\left(D_1\right)\Leftrightarrow a=-1;b\ne-7\Leftrightarrow\left(D_3\right):y=-x+b\\ \left(D_3\right)\cap\left(D_2\right)\text{tại điểm có tung độ }4\Leftrightarrow\left\{{}\begin{matrix}4=-3x+1\\4=-x+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\b=3\end{matrix}\right.\\ \text{Vậy }\left(D_3\right):y=-x+3\)
\(d,\Leftrightarrow B\left(4;-11\right)\in\left(D_4\right)\\ \Leftrightarrow8m-4-5m-2=-11\\ \Leftrightarrow3m=-5\Leftrightarrow m=-\dfrac{5}{3}\\ e,\Leftrightarrow\left\{{}\begin{matrix}-x-7=0\\\left(2m-1\right)x-5m-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-7\\7-14m-5m-2=0\end{matrix}\right.\\ \Leftrightarrow m=\dfrac{5}{19}\)



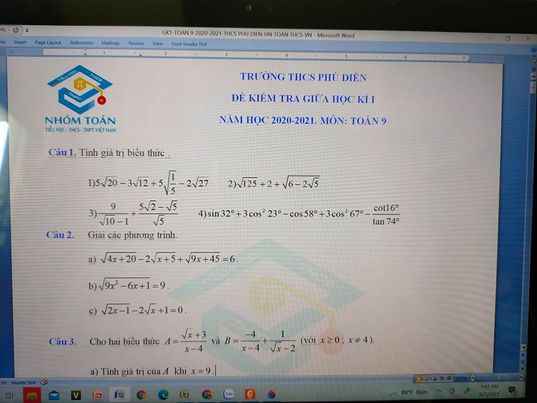
Câu 2: b. \(\sqrt{9x^2-6x+1}=9\)
<=> \(\sqrt{\left(3x-1\right)^2}=9\)
<=> 3x - 1 = 9
<=> 3x = 10
<=> x = \(\dfrac{10}{3}\)



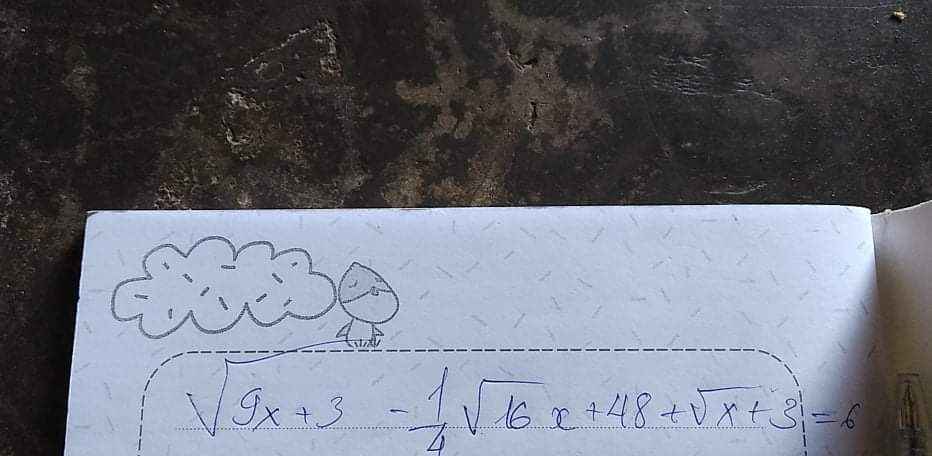




 Giải giúp mình bài 1 bài 2 đi mn
Giải giúp mình bài 1 bài 2 đi mn

Bài 1:
a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
b: Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD
Ta có: OA là đường trung trực của BC
=>OA\(\perp\)BC
Ta có: BC\(\perp\)CD
BC\(\perp\)OA
Do đó: CD//OA
c: Xét (O) có
AB,AC là tiếp tuyến
Do đó: OA là phân giác của góc BOC
=>\(\widehat{BOA}=\widehat{COA}=\dfrac{\widehat{BOC}}{2}=\dfrac{120^0}{2}=60^0\)
Xét ΔBOA vuông tại B có \(tanBOA=\dfrac{BA}{OB}\)
=>\(\dfrac{BA}{20}=tan60=\sqrt{3}\)
=>\(BA=20\sqrt{3}\left(cm\right)\)
Ta có: ΔBOA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(OA^2=\left(20\sqrt{3}\right)^2+20^2=1600\)
=>\(OA=\sqrt{1600}=40\left(cm\right)\)
Ta có: \(\widehat{BOC}+\widehat{DOC}=180^0\)(hai góc kề bù)
=>\(\widehat{DOC}+120^0=180^0\)
=>\(\widehat{DOC}=60^0\)
Xét ΔODC có OD=OC và \(\widehat{DOC}=60^0\)
nên ΔDOC đều
=>\(CD=OD=20\left(cm\right)\)
Câu 2:
a: Xét (A) có
AH là bán kính
BC\(\perp\)AH tại H
Do đó:BC là tiếp tuyến của (A)
Xét (A) có
BH,BD là các tiếp tuyến
Do đó:BH=BD và AB là phân giác của góc HAD
Xét (A) có
CH,CE là các tiếp tuyến
Do đó: CH=CE và AC là phân giác của góc HAE
Ta có: AB là phân giác của góc HAD
=>\(\widehat{HAD}=2\cdot\widehat{HAB}\)
AC là phân giác của góc HAE
=>\(\widehat{HAE}=2\cdot\widehat{HAC}\)
Ta có: \(\widehat{HAE}+\widehat{HAD}=\widehat{EAD}\)
=>\(\widehat{EAD}=2\cdot\widehat{HAB}+2\cdot\widehat{HAC}=2\left(\widehat{HAB}+\widehat{HAC}\right)\)
\(=2\cdot90^0=180^0\)
=>E,A,D thẳng hàng
b: Gọi O là trung điểm của BC
Ta có: ΔABC vuông tại A
mà AO là đường trung tuyến
nên AO=BO=CO
=>ΔBAC nội tiếp (O)
Xét hình thang BDEC có
O,A lần lượt là trung điểm của BC,DE
=>OA là đường trung bình của hình thang BDEC
=>OA//BD//EC
mà BD\(\perp\)AD
nên OA\(\perp\)AD
=>OA\(\perp\)ED
Xét (O) có
OA là bán kính
DE\(\perp\)OA tại A
Do đó: DE là tiếp tuyến của (O)
=>DE là tiếp tuyến của đường tròn đường kính BC