Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


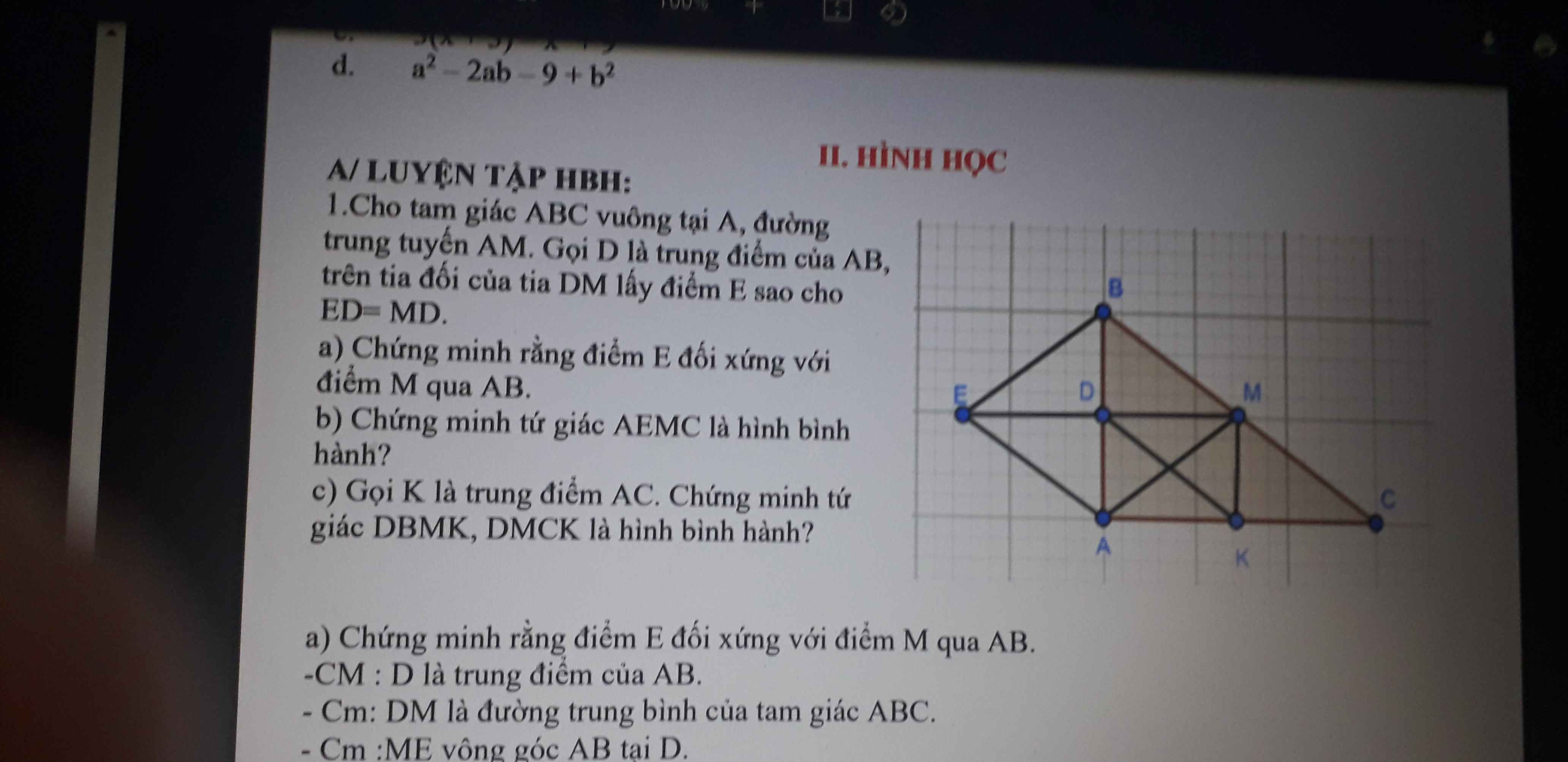
a) Xét tứ giác BDCE có:
BD//CE(cùng vuông góc AB)
BE//CD(cùng vuông góc AC)
=> BDCE là hình bình hành
b) Ta có: BDCE là hình bình hành
=> 2 đường chéo cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm BC
=> M là trung điểm DE
c) Gỉa sử DE đi qua A
Xét tam giác ABD và tam giác ACD lần lượt vuông tại B và C có:
AD chung
\(\widehat{ADB}=\widehat{ADC}\)(BDCE là hình bình hành)
=> ΔABD=ΔACD(ch-gn)
=> AB=AC
=> Tam giác ABC cân tại A
d) Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)(tổng 4 góc trong tứ giác)
\(\Rightarrow\widehat{A}=360^0-\widehat{B}-\widehat{C}-\widehat{D}\)
\(\Rightarrow\widehat{A}=360^0-90^0-90^0-\widehat{D}=180^0-\widehat{D}\)


a) Có vì ^ABC chung; ^AHB=^BAC=90
=> Tam giac ABC đồng dạng HBA(g-g)

Gọi a là đại diện số lẻ.Có m=2a vì m là số chẵn
=>m^3 +20m= (2a)^3+20*2a=8a^3+40a
Xét 8a^3+40a
1-8a^3+40a
=8a^3 -2a+42a
=(2a+1)(2a-1)2a+42a
(2a+1)(2a-1)2a chia hết cho 3(vì là tích 3 số nguyên liên tiếp)(1)
42a chia hết cho 3(2)
Từ (1)(2)=>(2a+1)(2a-1)2a+42a chia hết cho 3
=>8a^3+40a chia hết cho 3(3)
2-8a^3 + 40a
=8*(a^3+5)
=> 8a^3 + 40a chia hết cho 8(4)
Có a là số lẻ suy ra a^3 là số lẻ,suy ra a^3+5 là tổng 2 số lẻ nên là số chẵn
=>a^3+5 chia hết cho 2=>8a^3 + 40a chia hết cho 2(5)
Từ (3)(4)(5)=>8a^3+40a chia hết cho 48
=>m^3 +20m chia hết cho 48 với m là số chẵn
đúng nhé

c)\(\frac{a^2}{b^2}+\frac{b^2}{a^2}+4\ge3\cdot\left(\frac{a}{b}+\frac{b}{a}\right)\)
Thế : \(\frac{\left(a-b\right)^2\left(a^2-ab+b^2\right)}{a^2b^2}\ge0\)
\(\Leftrightarrow\frac{\left(b-a\right)^2\left(a^2-ab+b^2\right)}{a^2b^2}\ge0\)
\(\Leftrightarrow\frac{a^4+4a^2b^2+b^4}{a^2b^2}\ge\frac{3\left(a^2+b^2\right)}{ab}\)
\(\Leftrightarrow\frac{a^2}{b^2}+\frac{b^2}{a^2}+4\ge\frac{3a}{b}+\frac{3b}{a}\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)(luôn đúng)
\(\Rightarrow\frac{a^2}{b^2}+\frac{b^2}{a^2}+4>=3\cdot\left(\frac{a}{b}+\frac{b}{a}\right)\)

Áp dụng \(\left|A\right|+\left|B\right|\ge\left|A+B\right|\) khi \(AB\ge0\)
Ta có: \(\left|x-2016\right|+\left|x-2017\right|=\left|x-2016\right|+\left|2017-x\right|\ge\left|x-2016+2017-x\right|=1\)
Dấu "=" khi \(\left(x-2016\right)\left(2017-x\right)\ge0\Leftrightarrow2016\le x\le2017\)
Vậy khi \(2016\le x\le2017\) thì \(\left|x-2016\right|+\left|x-2017\right|=1\)

\(8a^3b-18a^3b^2\)
\(=2a^3b^2\left(4b-9\right)\)
Chú ý viết đề cẩn thận

2Giờ xe máy chạy được 70km. 3 giờ chạy được 105km ôtô chạy được 40km
mà 105+40=145 km
Vậy sau 3 giờ
 giúp em với
giúp em với