K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 10 2021
bn tìm ảnh của một điểm bất kì nằm trên đường thẳng qua phép tịnh tiến
vd : bn ra là m phẩy thông qua x và y r thay m phẩy vào phương trình cũ là ra
TG
mọi người giải giúp em theo phương pháp tự luận với ạ
2
22 tháng 8 2021
Câu 1: Ý C
PT \(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\) mà\(x\in\left(0;2\pi\right)\)
Có 3 nghiệm
Câu 2: Ý A
PT \(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\) mà \(0\le x< \dfrac{\pi}{2}\)
\(\Rightarrow x=\dfrac{\pi}{6}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
1.
\(y'=\left(cos^2\left(2x+3\right)\right)'=2cos\left(2x+3\right).\left(cos\left(2x+3\right)\right)'\)
\(=2cos\left(2x+3\right).\left(-sin\left(2x+3\right)\right).\left(2x+3\right)'\)
\(=-4sin\left(2x+3\right).cos\left(2x+3\right)\)
\(=-4sin\left(4x+6\right)\)
2.
\(f'\left(x\right)=-x^2+\left(3m-2\right)x-\left(2m^2-5m-2\right)\)
Để \(f'\left(x\right)< 0;\forall x\in R\)
\(\Leftrightarrow\Delta=\left(3m-2\right)^2-4\left(2m^2-5m-2\right)< 0\)
\(\Leftrightarrow m^2+8m+12< 0\)
\(\Rightarrow-6< m< -2\)
TG
0
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
1.
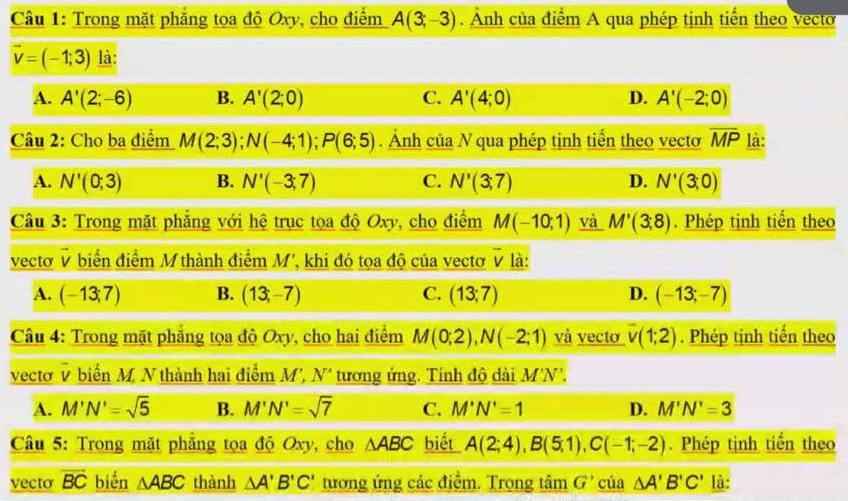
\(\left\{{}\begin{matrix}x_{A'}=x_A+\left(-1\right)=2\\y_{A'}=y_A+3=0\end{matrix}\right.\) \(\Rightarrow A'\left(2;0\right)\)
2.
\(\overrightarrow{MP}=\left(4;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{N'}=x_N+4=-4+4=0\\y_{N'}=y_N+2=1+2=3\end{matrix}\right.\)
\(\Rightarrow N'\left(0;3\right)\)
3.
\(\overrightarrow{MM'}=\left(13;7\right)\Rightarrow\overrightarrow{v}=\overrightarrow{MM'}=\left(13;7\right)\)
4.
\(\overrightarrow{MN}=\left(-2;-1\right)\Rightarrow MN=\sqrt{\left(-2\right)^2+\left(-1\right)^2}=\sqrt{5}\)
\(\Rightarrow M'N'=MN=\sqrt{5}\)
5.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(2;1\right)\)
\(\overrightarrow{BC}=\left(-6;-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=2-6=-4\\y_{G'}=1-3=-2\end{matrix}\right.\) \(\Rightarrow G'\left(-4;-2\right)\)
HP
12 tháng 9 2021
1.
\(2sinx+cosx=4\)
\(\Leftrightarrow\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sinx+\dfrac{1}{\sqrt{5}}cosx\right)=4\)
\(\Leftrightarrow sin\left(x+arccos\dfrac{2}{\sqrt{5}}\right)=\dfrac{4}{\sqrt{5}}>1\)
\(\Rightarrow2sinx+4cosx-4\ne0\)
Khi đó:
\(2P.sinx+P.cosx-4P=sinx-2cosx-3\)
\(\Leftrightarrow\left(2P-1\right)sinx+\left(P+2\right)cosx=4P-3\)
Phương trình có nghiệm khi:
\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(4P-3\right)^2\)
\(\Leftrightarrow4P^2-4P+1+P^2+4P+4\ge16P^2+9-24P\)
\(\Leftrightarrow11P^2-24P+4\le0\)
\(\Leftrightarrow\dfrac{2}{11}\le P\le2\)
\(\Rightarrow maxP=2\)
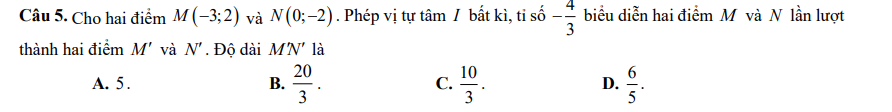
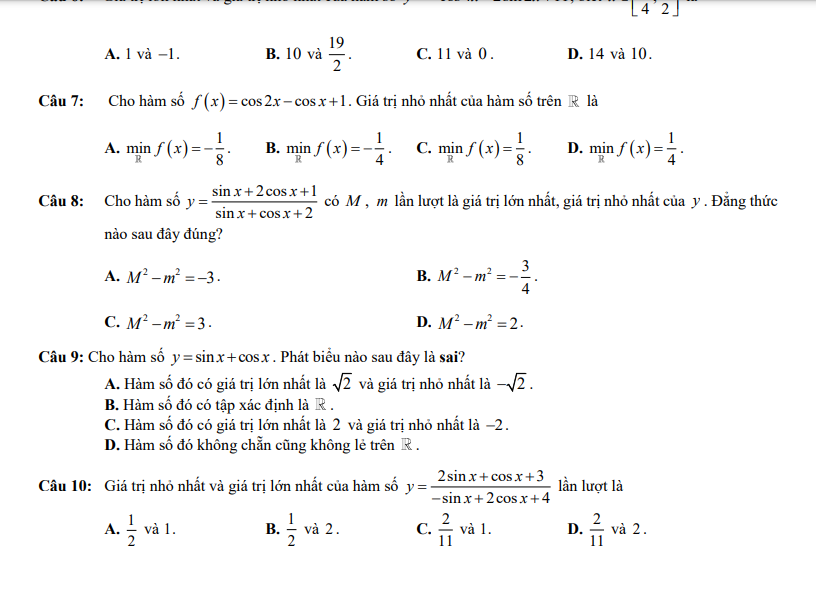
Do d' là ảnh của d qua phép tịnh tiến nên d' cùng phương với d
\(\Rightarrow\) Phương trình d' có dạng: \(x-2y+c=0\)
Chọn \(A\left(-1;0\right)\) là 1 điểm thuộc d
Gọi \(A'\left(x';y'\right)\) là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow A'\in d'\)
\(\left\{{}\begin{matrix}x'=-1+\left(-1\right)=-2\\y'=0+3=3\end{matrix}\right.\) \(\Rightarrow A'\left(-2;3\right)\)
Thế vào pt d':
\(-2-2.3+c=0\Rightarrow c=8\)
Vậy pt d' có dạng: \(x-2y+8=0\)