K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 10 2021
Bài 3:
\(a,=\dfrac{53\left(9+2\sqrt{7}\right)}{53}+2\sqrt{7}-5=9+2\sqrt{7}+2\sqrt{7}-5=4+4\sqrt{7}\)
24 tháng 10 2021
a: Sửa đề: \(\dfrac{53}{9-2\sqrt{7}}+2\sqrt{7}-5\)
\(=9+2\sqrt{7}+2\sqrt{7}-5\)
\(=4\sqrt{7}+4\)
23 tháng 10 2021
Bài 1:
a: \(-xy\sqrt{\dfrac{y}{x}}=-xy\cdot\dfrac{\sqrt{xy}}{x}=-y\sqrt{xy}\)
b: \(\sqrt{\dfrac{-3x^2}{35}}=\dfrac{\sqrt{105}x}{35}\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 3 2023
Do (d) đi qua E và G nên thay tọa độ E và G vào pt (d) ta được:
\(\left\{{}\begin{matrix}a.1+b=-3\\a.\left(-2\right)+b=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a+b=-3\\-2a+b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a=-9\\-2a+b=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-3\\b=0\end{matrix}\right.\)
Vậy pt (d) là: \(y=-3x\)
8 tháng 12 2021
\(a,B=4\sqrt{x+1}-3\sqrt{x+1}+\sqrt{x+1}+2\sqrt{x+1}=4\sqrt{x+1}\\ b,B=8\Leftrightarrow4\sqrt{x+1}=8\\ \Leftrightarrow\sqrt{x+1}=2\\ \Leftrightarrow x+1=4\\ \Leftrightarrow x=3\left(tm\right)\)
1 tháng 7 2023
8.31:
a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
XétΔBAC có BM/BA=BN/BC
nên MN//AC
=>MN vuông góc BD
=>MN vuông góc MQ
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc NMQ=90 độ
=>MNPQ là hình chữ nhật
=>M,N,P,Q cùng nằm trên 1 đường tròn
19 tháng 10 2021
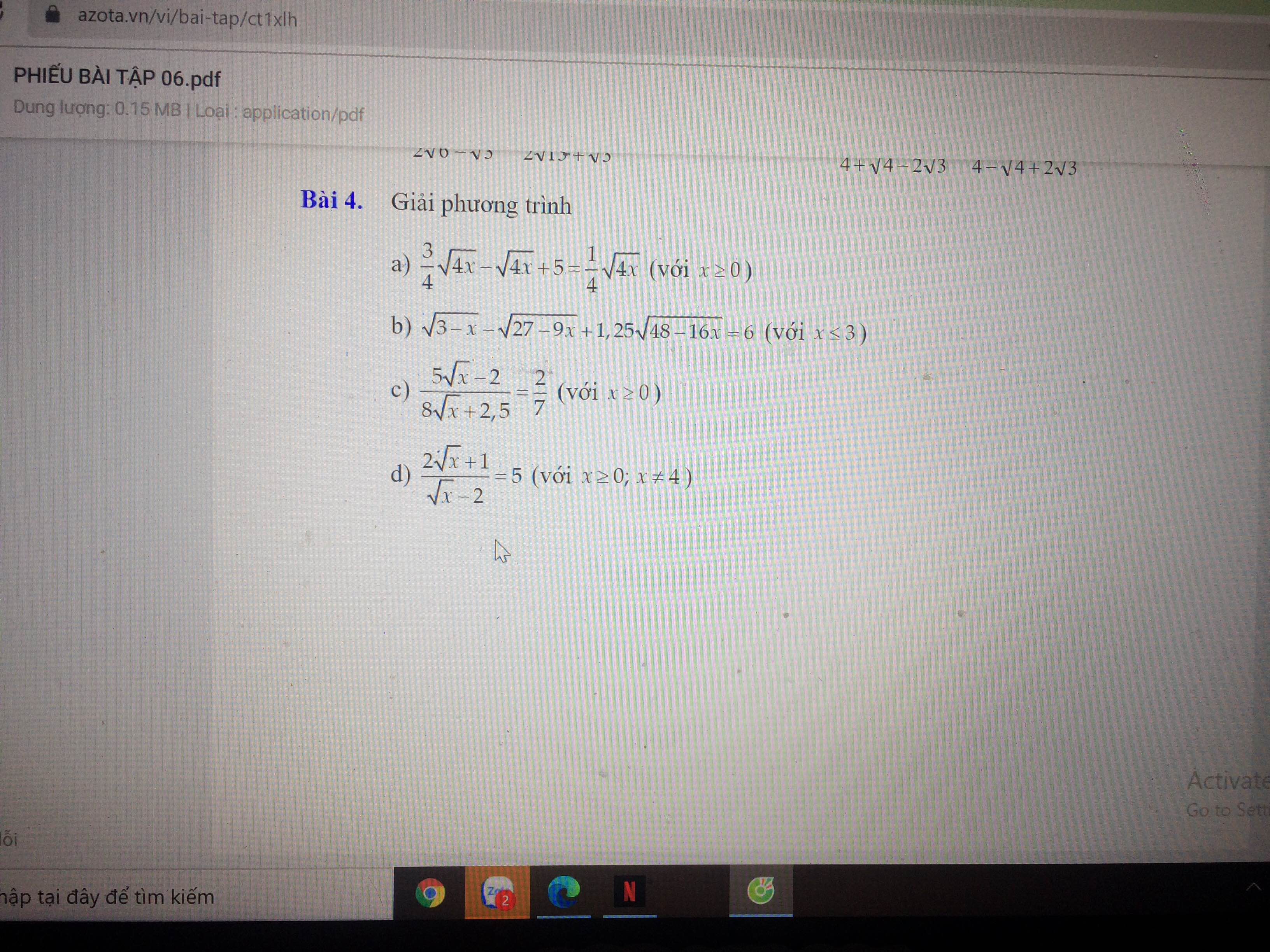
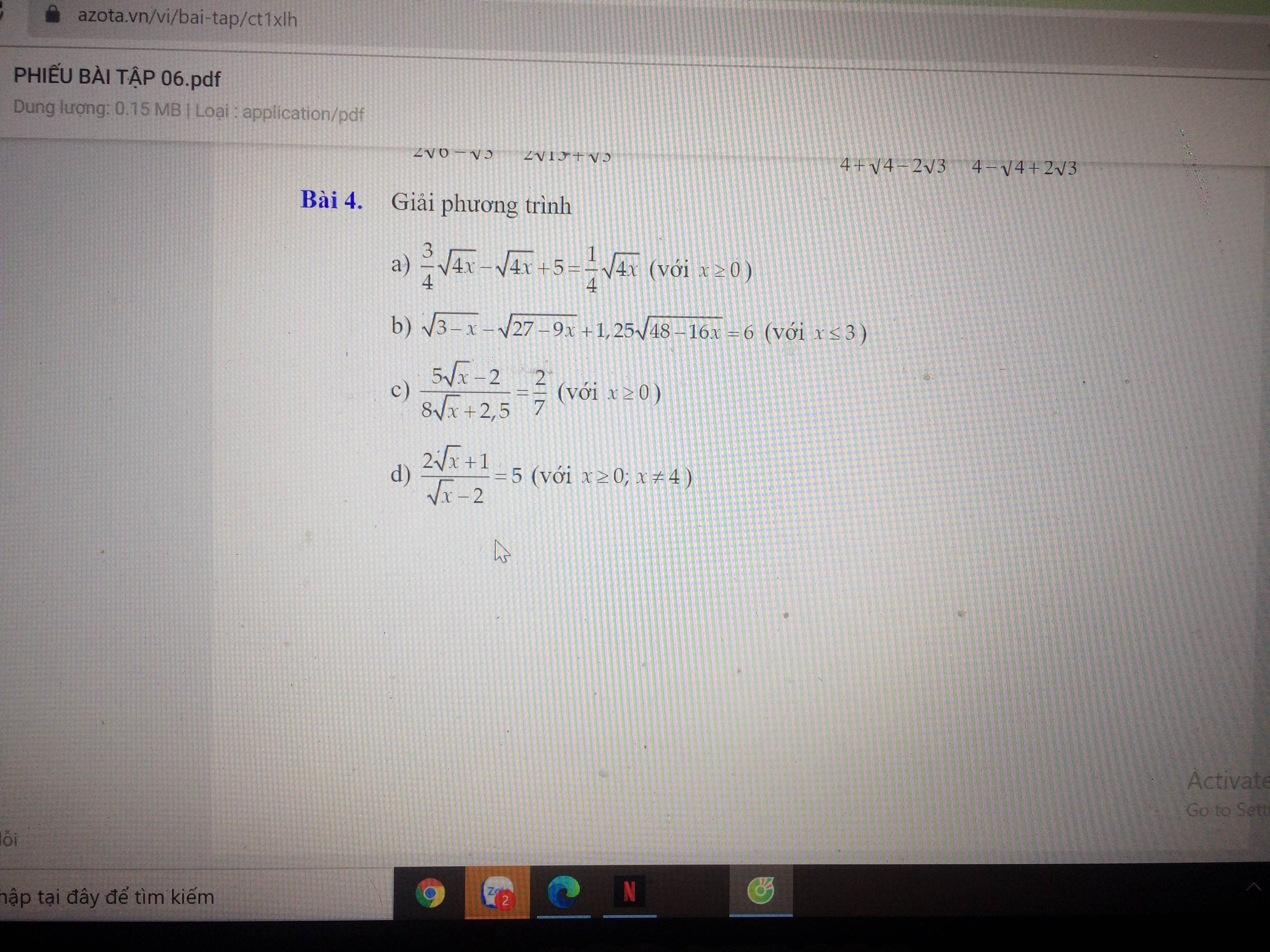
Bài 4:
d: Ta có: \(\dfrac{2\sqrt{x}+1}{\sqrt{x}-2}=5\)
\(\Leftrightarrow5\sqrt{x}-10=2\sqrt{x}+1\)
\(\Leftrightarrow3\sqrt{x}=11\)
hay \(x=\dfrac{121}{9}\)
23 tháng 10 2021
Bài 2:
a: \(\dfrac{2-\sqrt{3}}{3\sqrt{6}}=\dfrac{2\sqrt{6}-3\sqrt{2}}{18}\)
b: \(\dfrac{1}{\sqrt{3}+\sqrt{2}}=\sqrt{3}-\sqrt{2}\)
bài 3:
b: \(\dfrac{2}{\sqrt{3}+1}+\dfrac{1}{2-\sqrt{3}}+\dfrac{6}{3+\sqrt{3}}\)
\(=\sqrt{3}-1+2+\sqrt{3}+\sqrt{3}-1\)
\(=3\sqrt{3}\)