Giup em gap voi 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 11 2023
a: MNPQ là hình bình hành
=>MQ//NP
=>MQ//IP
Xét tứ giác MIPQ có IP//MQ
nên MIPQ là hình thang
b: ΔMNP vuông cân tại N
=>MN=NP và \(\widehat{MNP}=90^0\)
Hình bình hành MNPQ có \(\widehat{MNP}=90^0\)
nên MNPQ là hình chữ nhật
=>\(\widehat{Q}=\widehat{P}=90^0\)
Xét ΔMNI vuông tại N có \(sinNMI=\dfrac{NI}{MN}=\dfrac{2}{3}\)
nên \(\widehat{NMI}\simeq42^0\)
\(\widehat{NMI}+\widehat{QMI}=\widehat{NMQ}=90^0\)
=>\(\widehat{QMI}+42^0=90^0\)
=>\(\widehat{QMI}=48^0\)
IP//MQ
=>\(\widehat{QMI}+\widehat{MIP}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{MIP}+48^0=180^0\)
=>\(\widehat{MIP}=132^0\)
LA
7 tháng 3 2022
dễ mà bạn
a)3x-18=0 à mà mik chx hc phương trình
3x=18+0 sorry bạn nhé
3x=18
x=18:3
x=6
vậy x=6
SS
7 tháng 3 2022
a)\(3x-18=0\)
\(\Leftrightarrow3x=18\)
\(\Leftrightarrow x=6\)
Vậy x=6
b)\(2x.\left(x-4\right)-3x+12=0\)
\(\Leftrightarrow2x.\left(x-4\right)-3\left(x-4\right)=0\)
\(\Leftrightarrow\left(2x-3\right).\left(x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-3=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{2}\\x=4\end{cases}}}\)
Vậy .......
c)\(\frac{x-1}{2}-\frac{x+3}{3}=x+1\)
\(\Leftrightarrow6.\left(\frac{x-1}{2}-\frac{x+3}{3}\right)=6.\left(x+1\right)\)
\(\Leftrightarrow3.\left(x-1\right)-2.\left(x+3\right)=6x+6\)
\(\Leftrightarrow3x-3-2x-6=6x+6\)
\(\Leftrightarrow3x-2x-6x=6+3+6\)
\(\Leftrightarrow-5x=15\)
\(\Leftrightarrow x=-3\)
Vậy x= -3
d)\(\frac{x-3}{x+3}-\frac{5}{3-x}=\frac{30}{x^2-9}\)
\(\Leftrightarrow\frac{x-3}{x+3}-\frac{-5}{x-3}=\frac{30}{\left(x+3\right).\left(x-3\right)}\)
\(\Leftrightarrow\frac{\left(x-3\right).\left(x-3\right)}{\left(x+3\right).\left(x-3\right)}-\frac{-5.\left(x+3\right)}{\left(x-3\right).\left(x+3\right)}=\frac{30}{\left(x-3\right).\left(x+3\right)}\)
\(\Leftrightarrow\left(x-3\right)^2-\left(-5\right).\left(x+3\right)=30\)
\(\Leftrightarrow x^2-6x+9-\left(-5x-15\right)=30\)
\(\Leftrightarrow x^2-6x+9+5x+15-30=0\)
\(\Leftrightarrow x^2-x-6=0\)
\(\Leftrightarrow x^2-3x+2x-6=0\)
\(\Leftrightarrow x.\left(x-3\right)+2.\left(x-3\right)=0\)
\(\Leftrightarrow\left(x+2\right).\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=3\end{cases}}}\)
Vậy......
TB
1
VD
2
TG
21 tháng 8 2018
Ta có:(n-3)(n+3)-(n-7)(n-3) (1)
=(n-3)(n+3-n+7)
=10(n-3)
Vậy PT(1) chia hết cho 10
21 tháng 8 2018
\(\left(n-3\right)\left(n+3\right)-\left(n-7\right)\left(n-3\right)=\left(n-3\right)[n+3-\left(n-7\right)]\)
\(=\left(n-3\right)\left(n+3-n+7\right)=\left(n-3\right)\cdot10⋮10\)(ĐPCM)
PD
8
23 tháng 7 2015
\(4x^2-y^2+4x+1=\left(2x+1\right)^2-y^2=\left(2x+1-y\right)\left(2x+1+y\right)\)
may bai nay kho qua giup em , em dang can gap a
9 tháng 12 2023
Câu 2:
a: Không
b: Không
Câu 3:
a: \(\widehat{B}=\widehat{zAB}\left(=124^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên Bt//Az
b: n\(\perp\)DC
m\(\perp\)DC
Do đó: n//m
c: \(\widehat{xEG}+\widehat{yGE}=70^0+110^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ex//Gy
d: Vẽ lại hình, ta sẽ có:
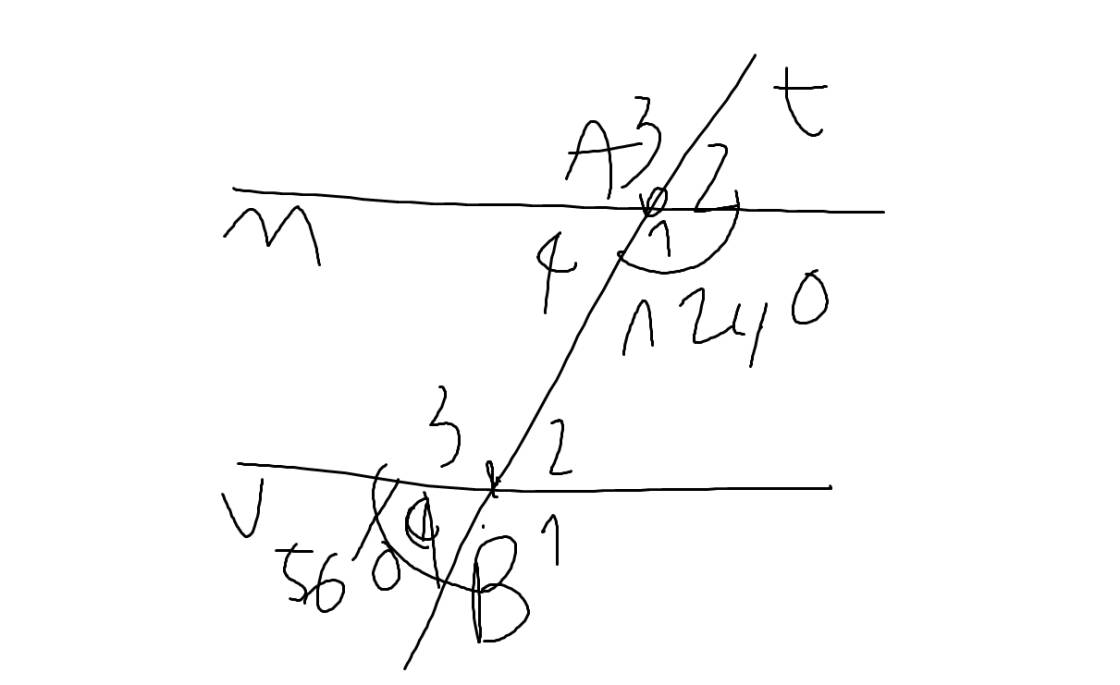
Ta có: \(\widehat{B_4}=\widehat{B_2}\)(hai góc đối đỉnh)
mà \(\widehat{B_4}=56^0\)
nên \(\widehat{B_2}=56^0\)
Ta có: \(\widehat{A_1}+\widehat{B_2}=124^0+56^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên m//v
HP
3
12 tháng 6 2018
5B=-25x2 -20x+5 = 9 - (25x2 +20x +4) = 9- (5x+2)2 \(\le9\)
=> B\(\le\frac{9}{5}\)<=> x=-2/5
HH
12 tháng 6 2018
Tìm GTLN của: \(B=-5x^2-4x+1\)
Ta có
\(B=-5x^2-4x+1\)
\(B=-5\left(x^2+\frac{4}{5}x-\frac{1}{5}\right)\)
\(B=-5\left[x^2+2x.\frac{2}{5}+\left(\frac{2}{5}\right)^2-\frac{4}{25}-\frac{5}{25}\right]\)
\(B=-5\left[\left(x+\frac{2}{5}\right)^2-\frac{9}{25}\right]\)
\(B=-5\left(x+\frac{2}{5}\right)^2+\frac{9}{5}\)
Mà \(-5\left(x+\frac{2}{5}\right)^2\le0\). Dấu "=" xảy ra khi và chỉ khi \(x=\frac{-2}{5}\)
=> \(-5\left(x+\frac{2}{5}\right)^2+\frac{9}{5}\le\frac{9}{5}\). Dấu "=" xảy ra khi và chỉ khi \(x=\frac{-2}{5}\)
Vậy B có GTLN bằng \(\frac{9}{5}\)khi \(x=\frac{-2}{5}\).
Tìm GTLN của: \(C=-2x^2+10x+3\)
Ta có
\(C=-2x^2+10x+3\)
\(C=-2\left(x^2-5x-\frac{3}{2}\right)\)
\(C=-2\left[x^2-2x.\frac{5}{2}+\left(\frac{5}{2}\right)^2-\frac{25}{4}-\frac{9}{4}\right]\)
\(C=-2\left[\left(x-\frac{5}{2}\right)^2-\frac{17}{2}\right]\)
\(C=-2\left(x-\frac{5}{2}\right)^2+17\)
Mà \(-2\left(x-\frac{5}{2}\right)^2\le0\). Dấu "=" xảy ra khi và chỉ khi \(x=\frac{5}{2}\)
=> \(-2\left(x-\frac{5}{2}\right)^2+17\le17\). Dấu "=" xảy ra khi và chỉ khi \(x=\frac{5}{2}\)
Vậy C có GTLN bằng 17 khi \(x=\frac{5}{2}\)
uiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiyhAAAAAAAAAAAAAAAAAAAAAAAAA