Giúp em câu d ạ. Please!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 1 2022
a: Xét ΔABM và ΔDBM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔABM=ΔDBM
b: Ta có: ΔABM=ΔDBM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
c: Ta có: BA=BD
nên ΔBAD cân tại B
mà BM là đường phân giác
nên BM là đường cao
d: Ta có: ΔABM=ΔDBM
nên MA=MD
Ta có: BA=BD
nên B nằm trên đường trung trực của AD(1)
Ta có: MA=MD
nên M nằm trên đường trung trực của AD(2)
Từ (1) và (2) suy ra BM là đường trung trực của AD
hay BM⊥AD
29 tháng 7 2021
b) Ta có: \(\left(-\dfrac{1}{2}\right)^2\cdot2\dfrac{6}{7}-\dfrac{14}{15}:2\dfrac{1}{3}+\left(-1.21\right)^0\)
\(=\dfrac{1}{4}\cdot\dfrac{20}{7}-\dfrac{14}{15}:\dfrac{7}{3}+1\)
\(=\dfrac{5}{7}-\dfrac{14}{15}\cdot\dfrac{3}{7}+1\)
\(=\dfrac{5}{7}-\dfrac{2}{5}+1\)
\(=\dfrac{25-14-35}{35}=\dfrac{-24}{35}\)
0H
Chỉ cần giải giúp em câu c,d thui ạ
1
24 tháng 5 2022
a: Xét ΔEAB có \(\widehat{EBA}=\widehat{EAB}\)
nên ΔEAB cân tại E
mà EK là đường cao
nen K là trung điểm của AB
hay KA=KB
b: Xét ΔACE vuông tại C và ΔBDE vuông tại D có
EA=EB
\(\widehat{AEC}=\widehat{BED}\)
Do đó: ΔACE=ΔBDE
Suy ra: EC=ED
Ta có: AE+ED=AD
BE+CE=BC
mà AE=BE
và ED=EC
nên AD=BC
NT
1
29 tháng 7 2021
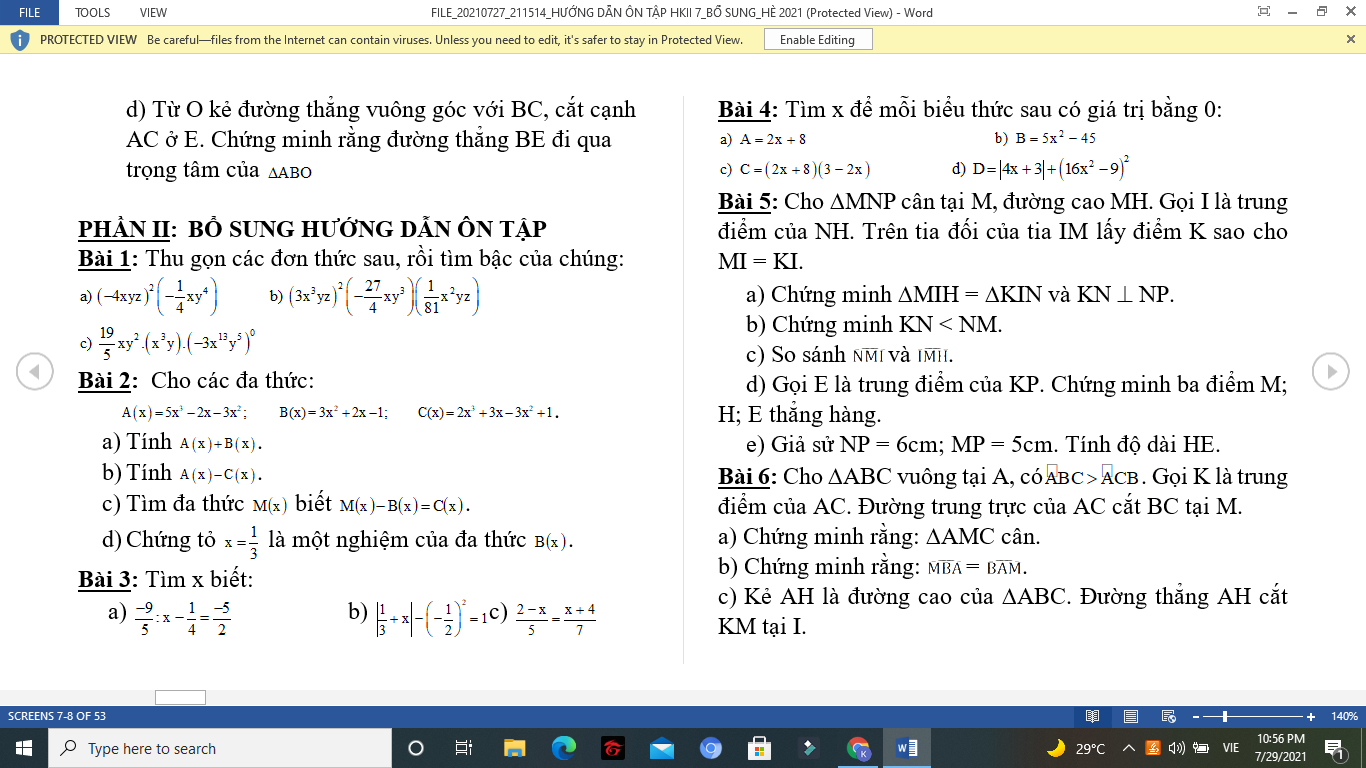
Bài 3:
c) Ta có: \(\dfrac{2-x}{5}=\dfrac{x+4}{7}\)
\(\Leftrightarrow14-7x=5x+20\)
\(\Leftrightarrow-7x-5x=20-14\)
\(\Leftrightarrow-12x=6\)
hay \(x=-\dfrac{1}{2}\)
d: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
SUy ra: DB=DC
hay D nằm trên đường trung trực của BC
mà AM là đường trung trực của BC
nên A,M,D thẳng hàng