K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 3 2023
a: ΔOCB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc CB
Vì góc OIA=góc OMA=góc ONA
nên O,M,N,I,A cùng thuộc 1 đường tròn
b: Xét ΔABN và ΔANC có
góc ABN=góc ANC
góc BAN chung
=>ΔABN đồng dạng với ΔANC
=>AB/AN=AN/AC
=>AN^2=AB*(AB+BC)
=>4*(BC+4)=6^2=36
=>BC=5cm
2 tháng 1 2022
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
CC
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 12 2020
\(a^3+b^3=\sqrt{\left(\sqrt{6}-\sqrt{2}\right)^2}-\dfrac{4\left(\sqrt{6}-\sqrt{2}\right)}{\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{6}-\sqrt{2}\right)}\)
\(=\sqrt{6}-\sqrt{2}-\dfrac{4\left(\sqrt{6}-\sqrt{2}\right)}{4}=0\)
\(\Rightarrow a=-b\Rightarrow a^5+b^5=0\)
HK
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
2
5 tháng 2 2022
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
SE
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
\(A=\sqrt{2a\left(b+1\right)}+\sqrt{2b\left(c+1\right)}+\sqrt{2c\left(a+1\right)}\)
\(A=\dfrac{1}{\sqrt{2}}\sqrt{4a\left(b+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4b\left(c+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4c\left(a+1\right)}\)
\(A\le\dfrac{1}{2\sqrt{2}}\left(4a+b+1\right)+\dfrac{1}{2\sqrt{2}}\left(4b+c+1\right)+\dfrac{1}{2\sqrt{2}}\left(4c+a+1\right)\)
\(A\le\dfrac{1}{2\sqrt{2}}\left[5\left(a+b+c\right)+3\right]=2\sqrt{2}\)
\(A_{max}=2\sqrt{2}\) khi \(a=b=c=\dfrac{1}{3}\)
29 tháng 5 2022
Đài ơi, giải giúp cho Sarah đi, tớ không có viết và giờ vào giường rồi , good nigh
DD
Đoàn Đức Hà
Giáo viên
28 tháng 5 2022
Câu 10:
Gọi \(H\) là giao điểm của \(MO\) và \(AB\).
Xét tam giác \(MAO\) vuông tại \(A\) đường cao \(AH\):
\(\dfrac{1}{AH^2}=\dfrac{1}{MA^2}+\dfrac{1}{AO^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{R\sqrt{2}}{2}\right)^2}=\dfrac{1}{MA^2}+\dfrac{1}{R^2}\Leftrightarrow MA=R\).
\(S_{MAOB}=S_{MAO}+S_{MBO}\)
\(=\dfrac{1}{2}.AO.MA+\dfrac{1}{2}.OB.MB\)
\(=\dfrac{1}{2}.R.R+\dfrac{1}{2}.R.R=R^2\)
Chọn C.
NP
0
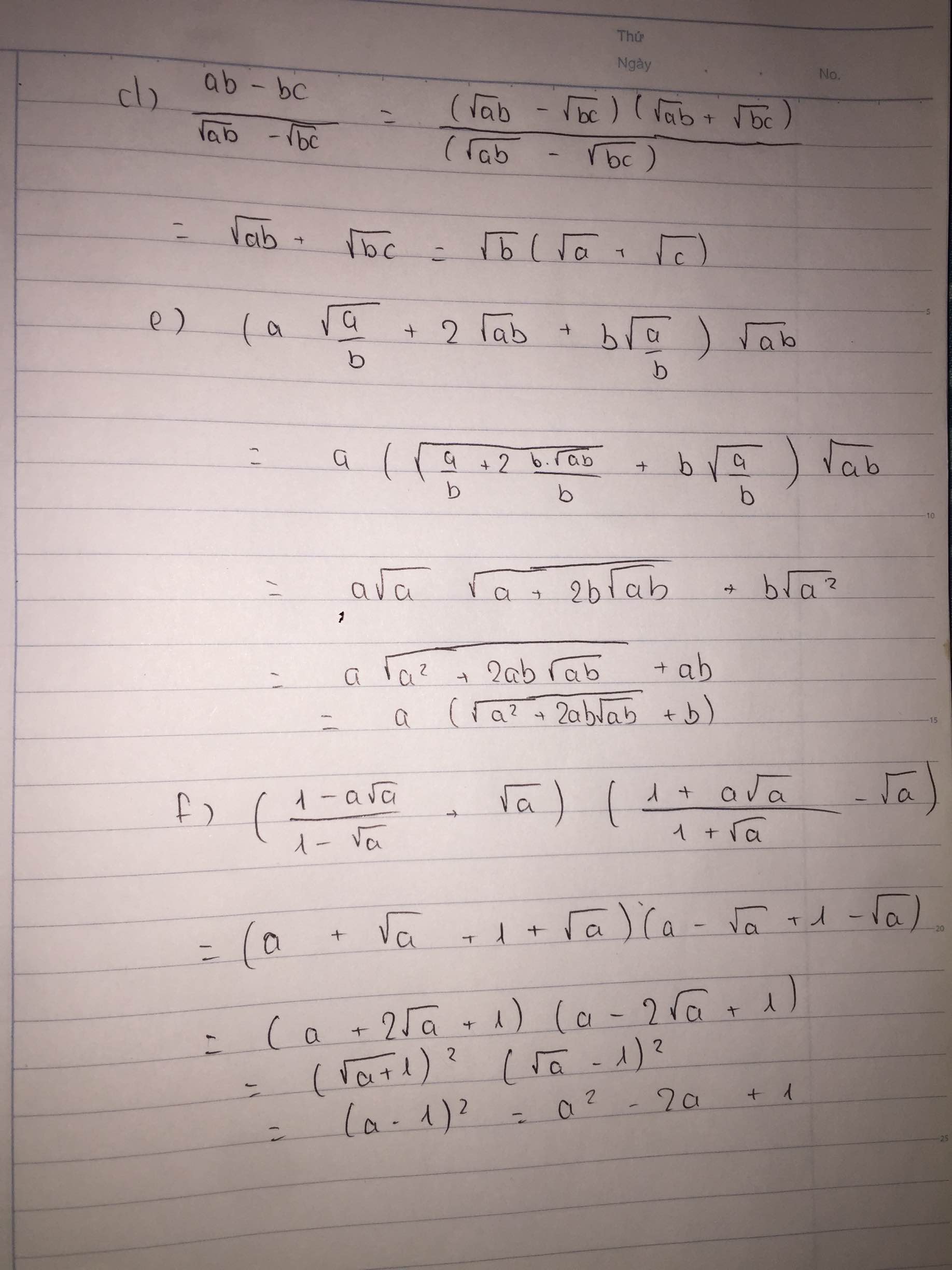
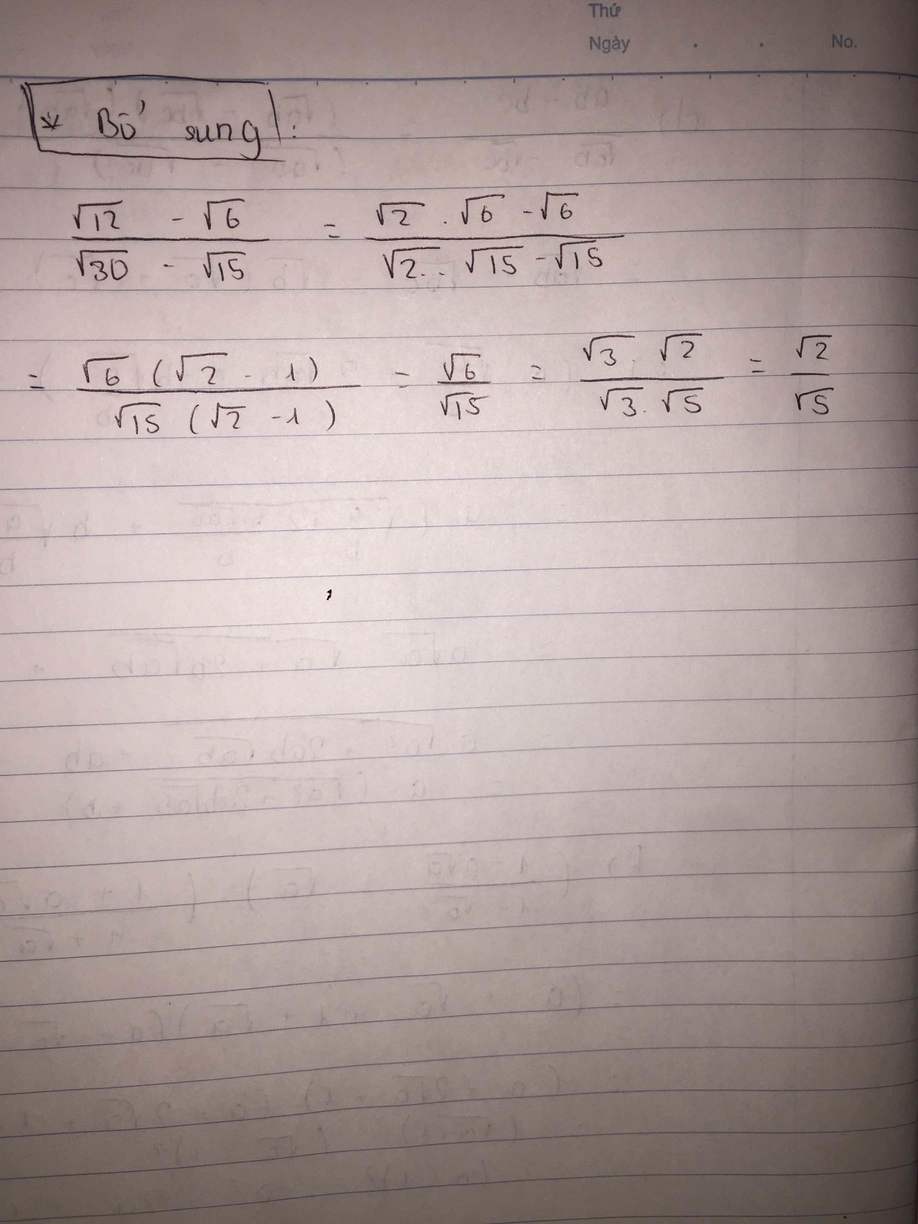
\(\Delta'=\left(m-1\right)^2-m^2\ge0\Rightarrow m\le\dfrac{1}{2}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2\end{matrix}\right.\)
\(x_1^2+2\left(m-1\right)x_2=15\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)-x_1x_2+2\left(m-1\right)x_2=15\)
\(\Leftrightarrow2\left(m-1\right)x_1+2\left(m-1\right)x_2-m^2=15\)
\(\Leftrightarrow2\left(m-1\right)\left(x_1+x_2\right)-m^2-15=0\)
\(\Leftrightarrow4\left(m-1\right)^2-m^2-15=0\)
\(\Leftrightarrow3m^2-8m-11=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=\dfrac{11}{3}>\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)