
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài AB và vận tốc dự kiến lần lượt là x,y
Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{10}{3}\\\dfrac{x}{y+5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-10y=0\\x-3y=15\end{matrix}\right.\)
=>x=150 và y=45


Ptr có `2` nghiệm phân biệt `<=>\Delta' > 0`
`=>(m+1)^2-m^2+2m-3 > 0`
`<=>m^2+2m+1-m^2+2m-3 > 0`
`<=>m > 1/2`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=2m+2),(x_1.x_2=c/a=m^2-2m+3):}`
Ta có: `1/[x_1 ^2]-[4x_2]/[x_1]+3x_2 ^2=0`
`=>1-4x_1.x_2+3(x_1.x_2)^2=0`
`<=>1-4(m^2-2m+3)+3(m^2-2m+3)^2=0`
`<=>[(m^2-2m+3=1),(m^2-2m+3=1/3):}`
`<=>[(m^2-2m+2=0(VN)),(m^2-2m+8/3=0(VN)):}`
`=>` Không có `m` thỏa mãn.

\(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\left(đk:x\ge0,x\ne9\right)\)
Để \(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}< 0\) thì
\(\sqrt{x}-3< 0\) ( do \(\sqrt{x}+3\ge3>0\))
\(\Leftrightarrow\sqrt{x}< 3\Leftrightarrow0\le x< 9\)
Mà \(x\in Z\)
\(\Rightarrow x\in\left\{0;1;2;3;4;5;6;7;8\right\}\)

a: Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=180^0\)
Do đó: AFHE là tứ giác nội tiếp
Xét tứ giác BFHD có
\(\widehat{BFH}+\widehat{BDH}=180^0\)
Do đó: BFHD là tứ giác nội tiếp
Xét tứ giác ECDH có
\(\widehat{HEC}+\widehat{HDC}=180^0\)
Do đó: ECDH là tứ giác nội tiếp
b: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
Xét tứ giác CDFA có
\(\widehat{CDA}=\widehat{CFA}=90^0\)
Do đó: CDFA là tứ giác nội tiếp

a) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
b) \(=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
c) \(=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)
d) \(=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
e) \(=\sqrt{\left(4-\sqrt{6}\right)^2}=4-\sqrt{6}\)
f) \(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)
l) \(=\sqrt{\left(\sqrt{2}-\dfrac{1}{2}\right)^2}=\sqrt{2}-\dfrac{1}{2}\)
m) \(=\sqrt{\left(2\sqrt{2}+\dfrac{1}{4}\right)^2}=2\sqrt{2}+\dfrac{1}{4}\)

bài 1:
\(\left\{{}\begin{matrix}x+y=57\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+4y=228\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6y=234\\x+y=57\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=39\\x=18\end{matrix}\right.\)
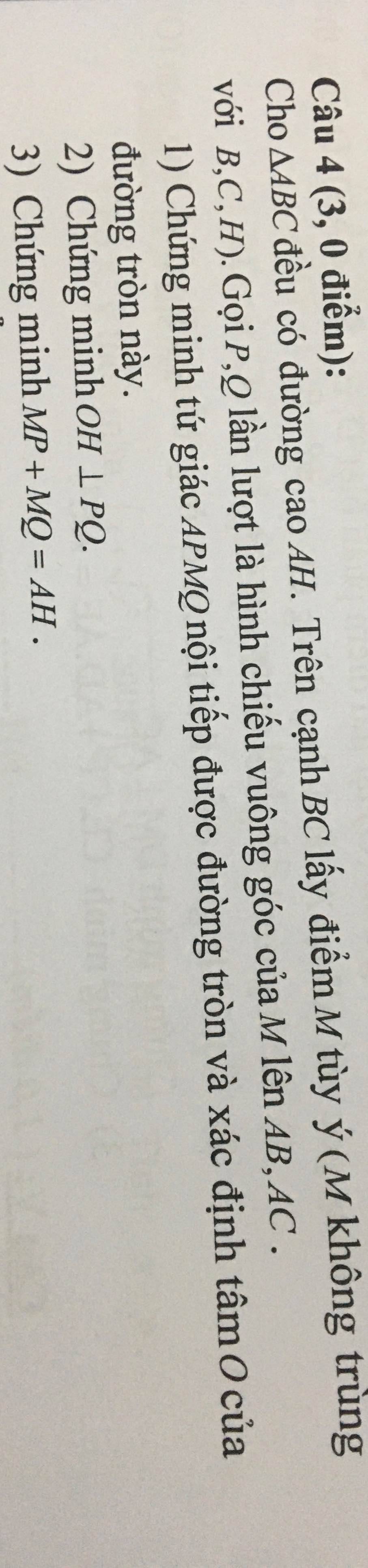






 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn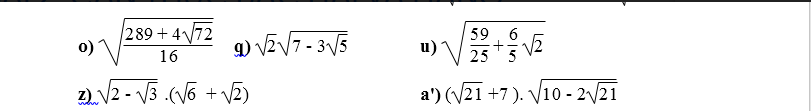


a: Xét tứ giác APMQ có \(\widehat{APM}+\widehat{AQM}=90^0+90^0=180^0\)
nên APMQ là tứ giác nội tiếp đường tròn đường kính AM
Tâm O là trung điểm của AM
b: Ta có: ΔAHM vuông tại H
=>H nằm trên đường tròn đường kính AM
=>H nằm trên (O)
Ta có: ΔABC đều
mà AH là đường cao
nên AH là phân giác của góc BAC
Xét (O) có
\(\widehat{PAH}\) là góc nội tiếp chắn cung PH
\(\widehat{QAH}\) là góc nội tiếp chắn cung QH
\(\widehat{PAH}=\widehat{QAH}\left(cmt\right)\)
Do đó: \(sđ\stackrel\frown{HP}=sđ\stackrel\frown{HQ}\)
Xét (O) có
\(\widehat{QPH}\) là góc nội tiếp chắn cung QH
\(\widehat{HQP}\) là góc nội tiếp chắn cung HP
\(sđ\stackrel\frown{QH}=sđ\stackrel\frown{HP}\)
Do đó: \(\widehat{HPQ}=\widehat{HQP}\)
=>HQ=HP
=>H nằm trên đường trung trực của QP(1)
Ta có: OP=OQ
=>O nằm trên đường trung trực của QP(2)
Từ (1) và (2) suy ra HO là đường trung trực của PQ
=>HO\(\perp\)PQ