
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB

a) \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^0\\sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\Rightarrow\widehat{C}=37^0\end{matrix}\right.\)
c) Ta có: \(\left\{{}\begin{matrix}AB=BD\\AC=DC\end{matrix}\right.\)(t/c 2 tiếp tuyến cắt nhau)
=> BC là đường trung trực AD
\(\Rightarrow AD\perp BC\)
Áp dụng HTL trong tam giác BDC vuông tại D:
\(FB.FC=FD^2\Rightarrow4FB.FC=4FD^2=\left(2FD\right)^2=AD^2\)

Hệ có nghiệm duy nhất khi \(m^2\ne1\Rightarrow m\ne\pm1\)
Khi đó: \(\left\{{}\begin{matrix}x+my=m+1\\m^2x+my=3m^2-m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+my=m+1\\\left(m^2-1\right)x=3m^2-2m-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3m+1}{m+1}\\y=\dfrac{m-1}{m+1}\end{matrix}\right.\)
Đặt \(P=xy=\dfrac{\left(3m+1\right)\left(m-1\right)}{\left(m+1\right)^2}=\dfrac{3m^2-2m-1}{\left(m+1\right)^2}=\dfrac{-\left(m+1\right)^2+4m^2}{\left(m+1\right)^2}\)
\(=-1+\left(\dfrac{2m}{m+1}\right)^2\ge-1\)
\(P_{min}=-1\) khi \(m=0\)

b: \(BC=\sqrt{89}\left(cm\right)\)
\(\sin\widehat{B}=\dfrac{5\sqrt{89}}{89}\)
\(\Leftrightarrow\widehat{B}\simeq32^0\)
\(\widehat{C}=58^0\)

ĐKXĐ: x>=0; x<>9
\(B=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{1}{\sqrt{x}+1}=\dfrac{-3}{\sqrt{x}+3}\)

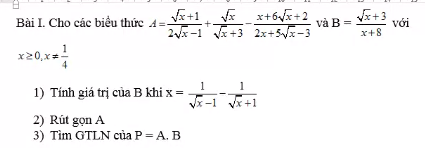





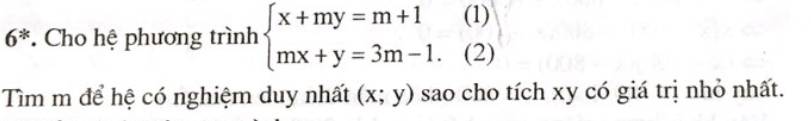


 Mọi người ơi,giúp em bài với ạ em cảm ơn ạ
Mọi người ơi,giúp em bài với ạ em cảm ơn ạ
Bài 10:
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền AB
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay AH=2,4(cm)
Bài 9:
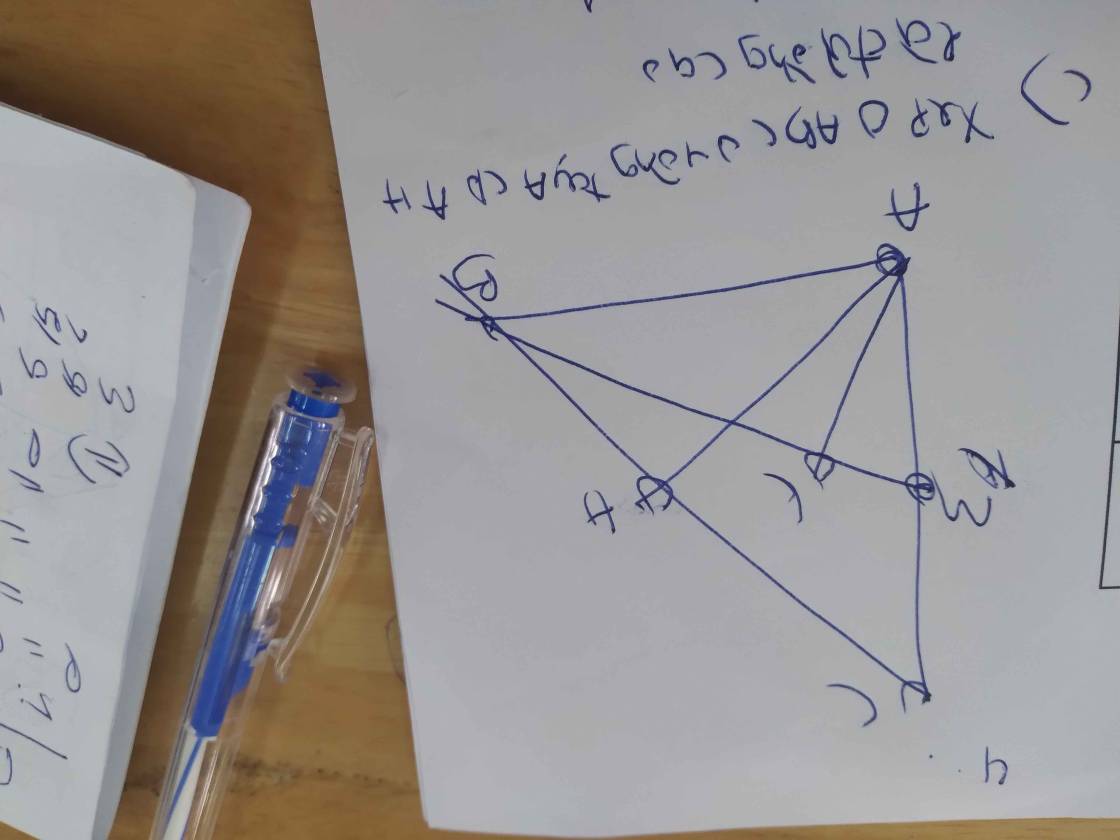
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{A}\) chung
Do đó: ΔABE\(\sim\)ΔACF
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{A}\) chung
Do đó: ΔAEF\(\sim\)ΔABC
b: Ta có: \(\dfrac{AE}{AB}=\dfrac{EF}{BC}\)
nên \(BC=EF:\dfrac{1}{2}=5:\dfrac{1}{2}=10\left(cm\right)\)