Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64

Đáp án A.
Xác suất một lần gieo được mặt một chấm là ![]() Xác suất để cả ba lần không gieo được mặt một chấm là
Xác suất để cả ba lần không gieo được mặt một chấm là 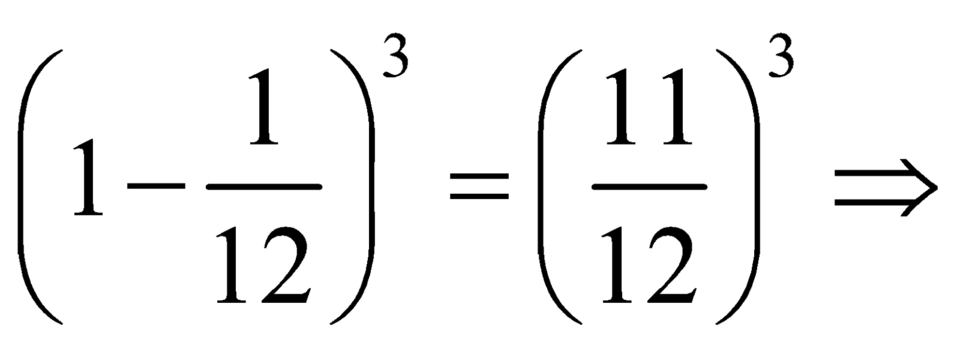 Xác suất để có ít nhất một lần gieo được mặt một chấm trong ba lượt gieo là:
Xác suất để có ít nhất một lần gieo được mặt một chấm trong ba lượt gieo là: 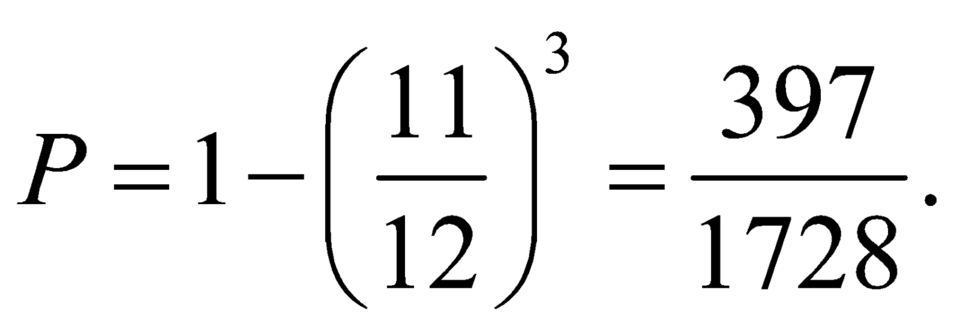

Không gian mẫu: \(\left\{SS;NN;SN;NS\right\}\)
Xác suất: \(P=\dfrac{2}{4}=\dfrac{1}{2}\)
sao 2/4 được ạ. xuất hiện mặt sấp đúng 1 lần chứ có phải là đúng lần 1 đâu mà biến cố là 2

Đáp án C
Gọi A k là biến cố lần thứ k xuất hiện mặt sấp
ta có P ( A k ) = 1 2 và
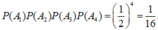

Chọn A
Ghi nhớ:
-Phép thử “gieo hai đồng tiền phân biệt” thì hai kết quả SN, NS của phép thử là khác nhau.
-Phép thử “gieo n đồng xu phân biệt” thì không gian mẫu có 2 n phần tử, với n ∈ ℕ * .

a. 1/8
b. 7/8
c. 3/8
(Ω) = { SSS,SSN,NSS,SNS,NNN,NNS,SNN,NSN}
⇒ n(Ω) = 8
a) Gọi Biến cố A= 'cả 3 đồng xu đều sấp'
➩ A = {SSS} ➩ n(A) = 1
➩ P(A) = n(A)/n(Ω) = 1/8
b) Gọi Biến cố B= 'có ít nhất 1 đồng xu sấp'
➩ B = { SNN,NNS,NSN,SSN,NSS,SNS,SSS } ➩ n(A) = 7
➩ P(B) = n(B)/n(Ω) = 7/8
c) Gọi Biến cố C = 'có đúng 1 đồng xu sấp '
➩ C = { SNN,NNS,NSN } ➩ n(C) = 3
➩ P(C) = n(C)/n(Ω) = 3/8