Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(sin\left(A\right)=\dfrac{BC}{AC}\Leftrightarrow sin\left(40^o\right)=\dfrac{BC}{8}\Leftrightarrow BC\approx5,14\left(cm\right)\)
\(cos\left(A\right)=\dfrac{AB}{AC}\Leftrightarrow cos\left(40^o\right)=\dfrac{AB}{8}\Leftrightarrow AB\approx6,12\left(cm\right)\)
b,
\(cotg\left(C\right)=\dfrac{BC}{AB}\Leftrightarrow\dfrac{1}{\sqrt{3}}=\dfrac{BC}{5}\Leftrightarrow BC=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
\(AC^2=AB^2+BC^2\Leftrightarrow AC=\sqrt{AB^2+BC^2}=\sqrt{5^2+\left(\dfrac{5\sqrt{3}}{3}\right)^2}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)

a: \(\widehat{C}=90^0-58^0=32^0\)
Xet ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}\)
nên \(AC=BC\cdot\sin B=72\cdot\sin58^0\simeq61,06\left(cm\right)\)
\(AB=\sqrt{BC^2-AB^2}=\sqrt{72^2-61.06^2}=38.15\left(cm\right)\)
b: \(\widehat{C}=90^0-48^0=42^0\)
Xét ΔABC vuông tại A có
\(AC=BC\cdot\cos C\)
nên \(BC=\dfrac{20}{\cos42^0}\simeq26.91\left(cm\right)\)
\(AB=\sqrt{26.91^2-20^2}=18.004\left(cm\right)\)
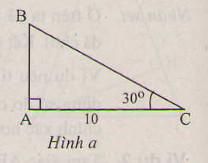
c: \(\widehat{B}=90^0-30^0=60^0\)
Xét ΔABC vuông tại A có
\(b=AC=BC\cdot\sin B\)
nên \(BC=\dfrac{AC}{\sin60^0}=\dfrac{15}{\sin60^0}=10\sqrt{3}\left(cm\right)\)
=>\(AB=\sqrt{\left(10\sqrt{3}\right)^2-15^2}=5\sqrt{3}\left(cm\right)\)

a: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*CB
=>AB^2/AC^2=BH/CH
b:
góc B=90-60=30 độ
góc HAB=90-30=60 độ
BC=căn 8^2+12^2=4*căn 13(cm)
HB=AB^2/BC=36/căn 13(cm)
AH=8*12/4*căn 13=24/căn 13(cm)

b, Có \(\widehat{C}=180^0-\widehat{A}-\widehat{C}=180^0-62^0-51^0=67^0\)
Kẻ AH \(\perp\)BC
Có \(\widehat{BAH}=90^0-\widehat{B}=90^0-51^0=39^0\)
Áp dụng ht trong tam giác vuông có:
\(BH=AB.sin\widehat{BAH}=10.sin39^0\approx6,29\left(cm\right)\)
\(AH=AB.sinB=10.sin51^0\)
\(sinC=\frac{AH}{AC}\)=> \(AC=\frac{AH}{sinC}=\frac{10.sin51^0}{sin67^0}\approx8,44\left(cm\right)\)
a, Có \(\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-30^0-42^0=108^0\)
Kẻ CH\(\perp\)AB
Xét tam giác vuông AHC có góc A bằng 300
=> \(CH=\frac{AC}{2}=\frac{4}{2}=2\)( vì trong tam giác vuông ,cạnh đối diện với góc 300 bằng một nửa cạnh huyền)
Áp dụng ht trong tam giác vuông có:
\(AH=AC.cos30^0=4.\frac{\sqrt{3}}{2}=2\sqrt{3}\) (cm)
\(HB=HC.cotB=2.cot42^0\approx2,22\)(cm)
=> AB=AH+HB=\(2\sqrt{3}+2,22\) (cm)
Áp dụng ht trong tam giác vuông có:
\(HC=BC.sinB\)
=> \(BC=\frac{HC}{sinB}=\frac{2}{sin51^0}\approx2,574\) (cm)