K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 6 2021
Ta có: \(\Delta'=32>0\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt
Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=12\\x_1x_2=4\end{matrix}\right.\)
Mặt khác: \(T=\dfrac{x_1^2+x^2_2}{\sqrt{x_1}+\sqrt{x_2}}\)
\(\Rightarrow T^2=\dfrac{x_1^4+x^4_2+2x_1^2x_2^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(x_1^2+x_1^2\right)^2}{x_1+x_2+2\sqrt{x_1x_2}}\) \(=\dfrac{\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(12^2-2\cdot4\right)^2}{12+2\sqrt{4}}=1156\)
Mà ta thấy \(T>0\) \(\Rightarrow T=\sqrt{1156}=34\)
CC
4
VN
11 tháng 3 2017
a) m = 2
=> x^2 + 2.2.x + 7 = 0
<=> x^2 + 4x + 7 = 0
( a = 1, b = 4, c = 7 )
\(\Delta\)= b^2 - 4ac
= 4^2 - 4.1.7
= -12 < 0
=> pt vô nghiệm
Ps: Coi lại đề nha bạn
15 tháng 8 2021
Ta có: \(x-\sqrt{4x^2-6x+9}=3\)
\(\Leftrightarrow\sqrt{4x^2-6x+9}=x-3\)
\(\Leftrightarrow4x^2-6x+9=x^2-6x+9\)
\(\Leftrightarrow x=0\left(loại\right)\)
GH
3 tháng 9 2023
\(\sqrt{\left(x^2-7\right)^2}=10\\ \Leftrightarrow\left|x^2-7\right|=10\left(1\right)\)
Nếu \(x^2\ge7\Leftrightarrow x\ge\sqrt{7}\) thì:
(1) \(\Leftrightarrow x^2-7=10\)
\(\Leftrightarrow x^2=10+7=17\\ \Leftrightarrow x=\left[{}\begin{matrix}\sqrt{17}\left(nhận\right)\\-\sqrt{17}\left(loại\right)\end{matrix}\right.\)
Nếu \(x^2< 7\Leftrightarrow x< \sqrt{7}\) thì:
(1) \(\Leftrightarrow7-x^2=10\)
\(\Leftrightarrow x^2=7-10=-3\left(loại\right)\)
Vậy PT có nghiệm \(x=\sqrt{17}\)
3 tháng 9 2023
\(\sqrt{\left(x^2-7\right)^2}=10\)
=>|x^2-7|=10
=>x^2-7=10 hoặc x^2-7=-10
=>x^2=17(nhận) hoặc x^2=-3(loại)
=>x^2=17
=>\(x=\pm\sqrt{17}\)
10 tháng 9 2016
\(3x-7\sqrt{x}+4=0\)
\(\left(3x-3\sqrt{x}\right)-\left(4\sqrt{x}-4\right)=0\)
\(3\sqrt{x}\left(\sqrt{x}-1\right)-4\left(\sqrt{x}-1\right)=0\)
\(\left(\sqrt{x}-1\right)\left(3\sqrt{x}-4\right)=0\)
\(\orbr{\begin{cases}x=1\\x=\frac{16}{9}\end{cases}}.\)
10 tháng 9 2016
Dễ mà:
3x-7Vx +4=3x-3Vx-4Vx+4=3Vx(Vx-1)-4Vx(Vx-1)=(Vx-1)(3Vx-4)=0
=>x=1,16/9
Note : V là căn
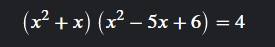
\(\Leftrightarrow x\left(x+1\right)\left(x-2\right)\left(x-3\right)=4\)
\(\Leftrightarrow\left(x^2-2x\right)\left(x^2-2x-3\right)=4\)
Đặt \(x^2-2x=t\)
\(\Rightarrow t\left(t-3\right)=4\)
\(\Leftrightarrow t^2-3t-4=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-2x=-1\\x^2-2x=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x+1=0\\x^2-2x-4=0\end{matrix}\right.\) (bấm máy)
cái đầu là sao em chx hiểu thầy