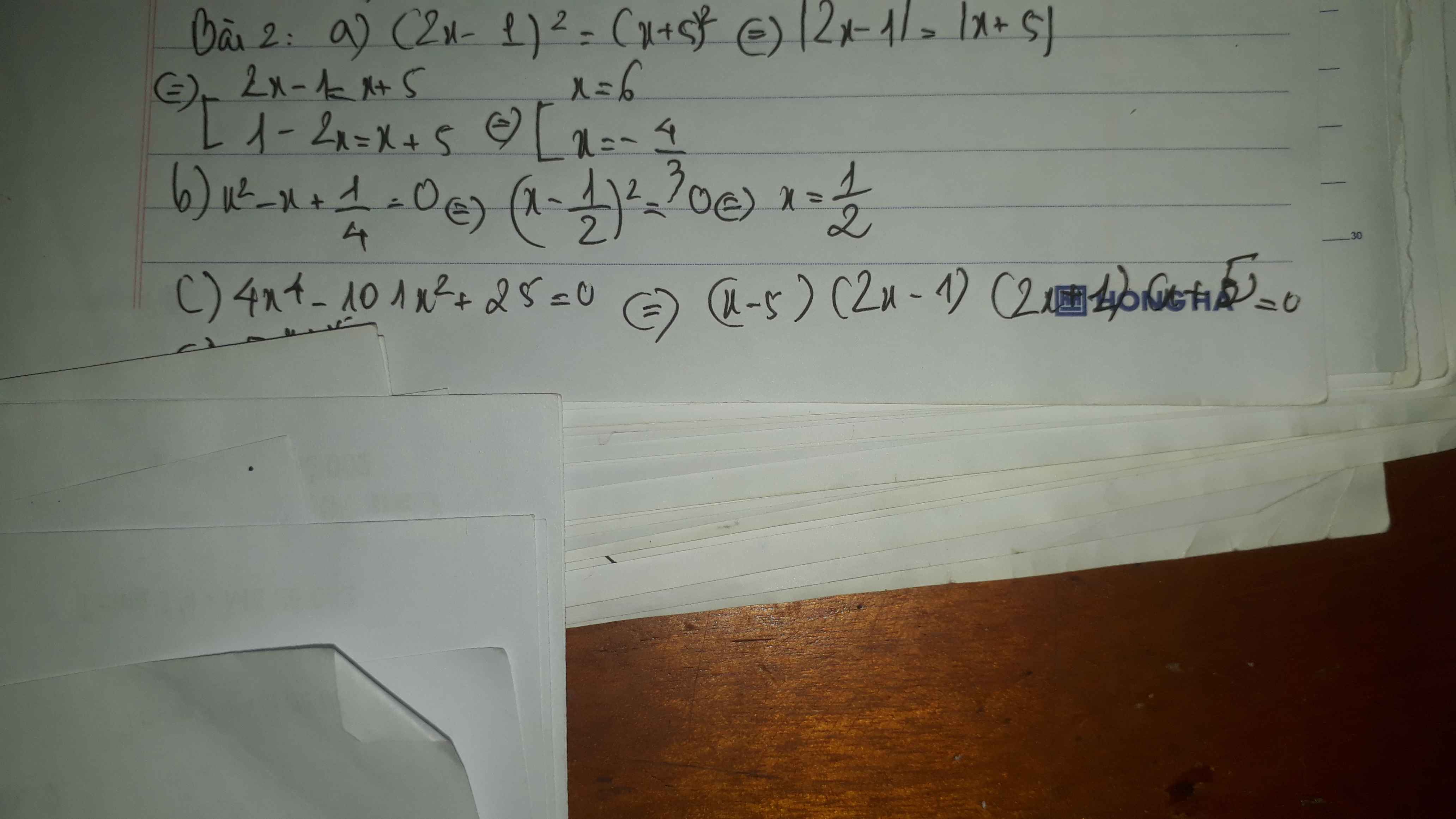Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) (3x - 2)(4x + 5) = 0
<=> 3x - 2 = 0 hoặc 4x + 5 = 0
<=> 3x = 2 hoặc 4x = -5
<=> x = 2/3 hoặc x = -5/4
b) (2,3x - 6,9)(0,1x + 2) = 0
<=> 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
<=> 2,3x = 6,9 hoặc 0,1x = -2
<=> x = 3 hoặc x = -20
c) (4x + 2)(x^2 + 1) = 0
<=> 4x + 2 = 0 hoặc x^2 + 1 # 0
<=> 4x = -2
<=> x = -2/4 = -1/2
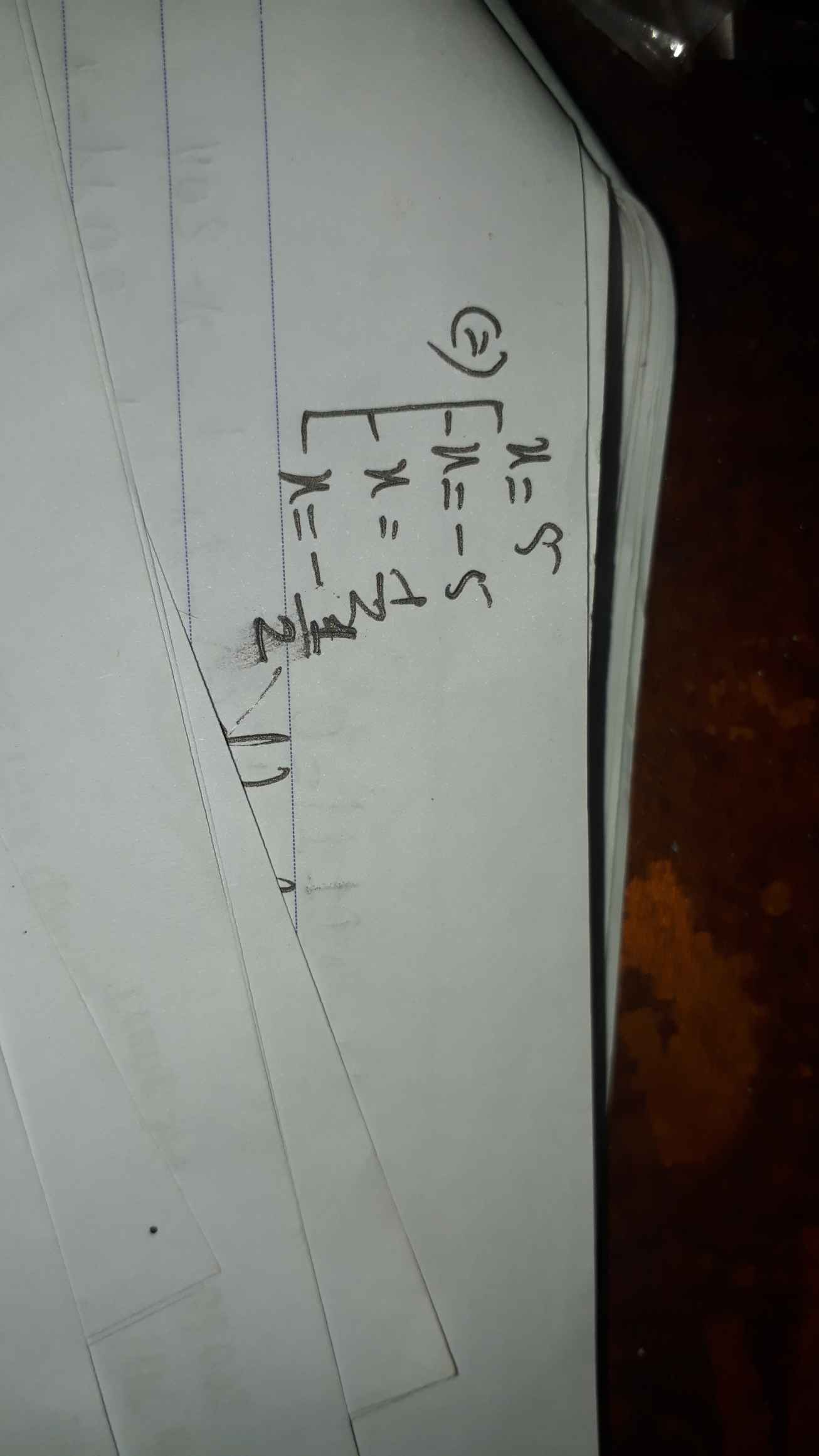
d) (2x + 7)(x - 5)(5x + 1) = 0
<=> 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
<=> 2x = -7 hoặc x = 5 hoặc 5x = -1
<=> x = -7/2 hoặc x = 5 hoặc x = -1/5

a: (3x-2)(4x+5)=0
=>3x-2=0 hoặc 4x+5=0
=>x=2/3 hoặc x=-5/4
b: (2,3x-6,9)(0,1x+2)=0
=>2,3x-6,9=0 hoặc 0,1x+2=0
=>x=3 hoặc x=-20
c: =>(x-3)(2x+5)=0
=>x-3=0 hoặc 2x+5=0
=>x=3 hoặc x=-5/2

1)(x2-4x+16)(x+4)-x(x+1)(x+2)+3x2=0
\(\Rightarrow\)(x3+64)-x(x2+2x+x+2)+3x2=0
\(\Rightarrow\)x3+64-x3-2x2-x2-2x+3x2=0
\(\Rightarrow\)-2x+64=0
\(\Rightarrow\)-2x=-64
\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)
\(\Rightarrow x=32\)
2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50
\(\Rightarrow\)8x-24x2+2-6x+24x2-60x-4x+10=50
\(\Rightarrow\)-62x+12=50
\(\Rightarrow\)-62x=50-12
\(\Rightarrow\)-62x=38
\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)

\(a,x^2-10x=-25\)
\(< =>x^2-10x+25=0\)
\(< =>\left(x-5\right)^2=0< =>x=5\)
b, \(4x^2-4x=-1\)
\(< =>4x^2-4x+1=0\)
\(< =>\left(2x-1\right)^2=0< =>x=\frac{1}{2}\)

1) \(\left(\dfrac{1}{2}x+3\right)\left(x^2-4x-6\right)\)
\(=\dfrac{1}{2}x^3-2x^2-3x+3x^2-12x-18\)
\(=\dfrac{1}{2}x^3+x^2-15x-18\)
2) \(\left(6x^2-9x+15\right)\left(\dfrac{2}{3}x+1\right)\)
\(=4x^3+6x^2-6x^2-9x+10x+15\)
\(=4x^3+x+15\)
3) Ta có: \(\left(3x^2-x+5\right)\left(x^3+5x-1\right)\)
\(=3x^5+15x^2-3x^2-x^4-5x^2+x+5x^3+25x-5\)
\(=3x^5-x^4+5x^3+10x^2+26x-5\)
4) Ta có: \(\left(x-1\right)\left(x+1\right)\left(x-2\right)\)
\(=\left(x^2-1\right)\left(x-2\right)\)
\(=x^3-2x^2-x+2\)

Lời giải:
PT $\Leftrightarrow (x^2-1)^3+(x^2+2)^3+(2x-1)^3-3(x^2-1)(x^2+2)(2x-1)=0$
Đặt $x^2-1=a; x^2+2=b; 2x-1=c$ thì pt trở thành:
$a^3+b^3+c^3-3abc=0$
$\Leftrightarrow (a+b)^3+c^3-3ab(a+b)-3abc=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)=0$
$\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0$
$\Rightarrow a+b+c=0$ hoặc $a^2+b^2+c^2-ab-bc-ac=0$
Nếu $a+b+c=0$
$\Leftrightarrow x^2-1+x^2+2+2x-1=0$
$\Leftrightarrow 2x^2+2x=0$
$\Rightarrow x=0$ hoặc $x=-1$
Nếu $a^2+b^2+c^2-ab-bc-ac=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
$\Rightarrow a-b=b-c=c-a=0$ (dễ CM)
$\Leftrightarrow a=b=c$
$\Leftrightarrow x^2-1=x^2+2=2x-1$ (vô lý)
Vậy..........
Akai Haruma Chị ơi chỗ
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\) từ chỗ trên chị tách làm sao ra được vế beeb phải vậy ạ

Bài 1
a/ \(x\left(x^2+1\right)+2\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+1\right)=0\Rightarrow x=-2\)
b/
\(\Leftrightarrow x^3-6x^2+9x+5x^2-30x+45=0\)
\(\Leftrightarrow x\left(x-3\right)^2+5\left(x-3\right)^2=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-3\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=3\end{matrix}\right.\)
1.
c/ \(\Leftrightarrow x^3+2x^2+2x+x^2+2x+2=0\)
\(\Leftrightarrow x\left(x^2+2x+2\right)+x^2+2x+2=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+2=0\left(vn\right)\end{matrix}\right.\)
d/
\(\Leftrightarrow x^4+x^3-2x^2-x^3-x^2+2x+4x^2+4x-8=0\)
\(\Leftrightarrow x^2\left(x^2+x-2\right)-x\left(x^2+x-2\right)+4\left(x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x^2-x+4\right)\left(x^2+x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-x+4=0\left(vn\right)\\x^2+x-2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
 Bài 1.
Bài 1.