K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 3 2021
\(5x^2+4x+2x^3+x^4-12=0\)
\(\Leftrightarrow x^4+2x^3+5x^2+4x-12=0\)
\(\Leftrightarrow x^4-x^3+3x^3-3x^2+8x^2-8x+12x-12=0\)
\(\Leftrightarrow x^3\left(x-1\right)+3x^2\left(x-1\right)+8x\left(x-1\right)+12\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^3+3x^2+8x+12\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^3+2x^2+x^2+2x+6x+12\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^2\left(x+2\right)+x\left(x+2\right)+6\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2+x+6\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[x^2+2\times\dfrac{1}{2}x+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{1}{2}\right)^2+6\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+\dfrac{1}{2}\right)^2+\dfrac{23}{4}\right]\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x+2=0\\\left(x^2+\dfrac{1}{2}\right)^2+\dfrac{23}{4}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Vì \(\left(x^2+\dfrac{1}{2}\right)^2\ge0\forall x\Rightarrow\left(x^2+\dfrac{1}{2}\right)^2+\dfrac{23}{4}\ge\dfrac{23}{4}\forall x\)
\(\Rightarrow\left(x^2+\dfrac{1}{2}\right)^2+\dfrac{23}{4}\) vô nghiệm
Vậy phương trình có tập nghiệm là\(S=\left\{1;-2\right\}\)
PT
1
CM
22 tháng 3 2018
2x3 + 5x2 – 3x = 0
⇔ x(2x2 + 5x – 3) = 0
⇔ x.(2x2 + 6x – x – 3) = 0
⇔ x. [2x(x + 3) – (x + 3)] = 0
⇔ x.(2x – 1)(x + 3) = 0
⇔ x = 0 hoặc 2x – 1 = 0 hoặc x + 3 = 0
+ 2x – 1 = 0 ⇔ 2x = 1 ⇔ x = 1/2.
+ x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm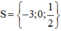 
10 tháng 8 2021
d: Ta có: \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)=24\)
\(\Leftrightarrow\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24=0\)
\(\Leftrightarrow x\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
NH
3
18 tháng 8 2021
a: \(\dfrac{2x^3-5x^2-x+1}{2x+1}\)
\(=\dfrac{2x^3+x^2-6x^2-3x+2x+1}{2x+1}\)
\(=x^2-3x+1\)
b: \(\dfrac{x^3-2x+4}{x+2}\)
\(=\dfrac{x^3+2x^2-2x^2-4x+2x+4}{x+2}\)
\(=x^2-2x+2\)
27 tháng 7 2021
c) Ta có: \(\dfrac{5x^4+9x^3-2x^2-4x-8}{x-1}\)
\(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=\dfrac{5x^3\left(x-1\right)+14x^2\left(x-1\right)+12x\left(x-1\right)+8\left(x-1\right)}{x-1}\)
\(=5x^3+14x^2+12x+8\)
d) Ta có: \(\dfrac{5x^3+14x^2+12x+8}{x+2}\)
\(=\dfrac{5x^3+10x^2+4x^2+8x+4x+8}{x+2}\)
\(=\dfrac{5x^2\left(x+2\right)+4x\left(x+2\right)+4\left(x+2\right)}{x+2}\)
\(=5x^2+4x+4\)
27 tháng 7 2021
c) Ta có: \(\dfrac{5x^4+9x^3-2x^2-4x-8}{x-1}\)
\(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=\dfrac{5x^3\left(x-1\right)+14x^2\left(x-1\right)+12x\left(x-1\right)+8\left(x-1\right)}{x-1}\)
\(=5x^3+14x^2+12x+8\)
DX
1
31 tháng 10 2021
b: \(\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}\)
\(=x^2-2x+1\)
\(=\left(x-1\right)^2\)
c: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=5x^3+14x^2+12x+8\)
Hoặc bạn có thể dùng mẹo: Thấy tổng các hệ số bậc chẵn bằng tổng các hệ số bậc lẻ nên PT chắc chắn có nghiệm $x=-1$
Phân tích đa thức để xuất hiện nhân tử $(x+1)$.
Lời giải:
$x^4-2x^3+5x^2-4x-12=0$
$\Leftrightarrow (x^4-2x^3+x^2)+4(x^2-x)-12=0$
$\Leftrightarrow (x^2-x)^2+4(x^2-x)-12=0$
$\Leftrightarrow (x^2-x)^2+4(x^2-x)^2+4-16=0$
$\Leftrightarrow (x^2-x+2)^2-4^2=0$
$\Leftrightarrow (x^2-x+2-4)(x^2-x+2+4)=0$
$\Leftrightarrow (x^2-x-2)(x^2-x+6)=0$
$\Leftrightarrow (x+1)(x-2)(x^2-x+6)=0$
Dễ thấy $x^2-x+6=(x-\frac{1}{2})^2+\frac{23}{4}>0$ nên $(x+1)(x-2)=0$
$\Rightarrow x=-1$ hoặc $x=2$