NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CN
2
B
1 tháng 11 2020
ĐK : \(x\ge0\)
\(x+1+\sqrt{x^2-4x+1}=3\sqrt{x}\Leftrightarrow \left ( 2x+2-5\sqrt{x} \right )+\left ( 2\sqrt{x^2-4x+1}-\sqrt{x} \right )=0\)
\(\Leftrightarrow\)\(\left ( 4x^2-17x+4 \right )\left ( \frac{1}{2x+2+5\sqrt{x}}+\frac{1}{2\sqrt{x^2-4x+1}+\sqrt{x}} \right )=0\)
\(\Leftrightarrow 4x^2-17x+4=0\Leftrightarrow x=4\)
NK
0
VL
0
NM
0
PM
0
PT
1
CM
30 tháng 3 2019
Điều kiện xác định:
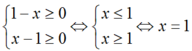
Xét x = 1: VT (2) = 1; VP (2) = 2.
Vậy x = 1 không phải nghiệm của (2) nên phương trình (2) vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
DT
1
7 tháng 5 2016
Phương trình đã cho tương đương với :
\(\left(2^{2^x}-2^{x+1}\right)+\left(3^{2^x}-3^{x+1}\right)=x+1-2^x\)
Ta xét các trường hợp sau :
* Nếu \(2^x>x+1\) thì \(2^{2^x}-2^{x+1}>0;3^{2^x}-3^{x+1}>0;x+1-2^x< 0\) nên phương trình đã cho không thỏa mãn.
* Nếu \(2^x< x+1\) thì \(2^{2^x}-2^{x+1}< 0;3^{2^x}-3^{x+1}< 0;x+1-2^x>0\) nên phương trình đã cho không thỏa mãn.
* Nếu \(2^x=x+1\) thì phương trình đã cho thỏa mãn và khi đó nghiệm của nó cũng là nghiệm của \(2^x=x+1\)
Xét hàm số \(f\left(t\right)=2^t-\left(t+1\right)\) ta thấy \(f'\left(t\right)=2^t.\ln2-1;f"\left(t\right)=2^t\left(\ln2\right)^2>0\) nên phương trình có không quá 2 nghiệm phân biệt
Ta lại thấy \(f\left(0\right)=f\left(1\right)=0\) nên phương trình \(f\left(t\right)=0\) có đúng 2 nghiệm là 0 và 1
Vậy phương trình đã cho có 2 nghiệm là \(x=0;x=1\)
\(\sqrt{x^2-x-1}=\sqrt{x-1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\x^2-x-1=x-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x^2-2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow x=2\)