Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)

Đáp án: D
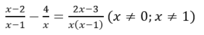
![]() có hai nghiệm là
có hai nghiệm là ![]() . Ta thấy
. Ta thấy ![]() không thỏa mãn điều kiện của phương trình
không thỏa mãn điều kiện của phương trình 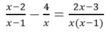 nên
nên ![]() không là nghiệm của phương trình
không là nghiệm của phương trình 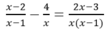 hay
hay ![]() là nghiệm ngoại lai.
là nghiệm ngoại lai.


Viết lại phương trình dưới dạng :
\(4^{x^2-3x+2}+4^{2x^2+6x+5}=4^{x^2-3x+2}.4^{2x^2+6x+5}+1\)
Đặt \(\begin{cases}u=4^{x^2-3x+2}\\v=4^{2x^2+6x+5}\end{cases}\)\(;u,v>0\)
Khi đó phương trình tương đương với :
\(u+v=uv+1\Leftrightarrow\left(u-1\right)\left(1-v\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}u=1\\v=1\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}4^{x^2-3x+2}=1\\4^{2x^2+6x+5}=1\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x^2-3x+2=0\\2x^2+6x+5=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=1\\x=2\\x=-1\\x=-5\end{array}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+2x-3\ge0\\2x^2-3x+1\ge0\\x^2+2x-3\le2x^2-3x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge1\\x\le-3\end{matrix}\right.\\\left[{}\begin{matrix}x\ge1\\x\le\dfrac{1}{2}\end{matrix}\right.\\x^2-5x+4\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge1\\x\le-3\end{matrix}\right.\\\left[{}\begin{matrix}x\ge4\\x\le1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x\le-3\\x\ge4\end{matrix}\right.\)

(2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x2 – 5
⇔ 2x2 + 6x - x – 3 – 3x + 1 ≤ x2 + 3x - x – 3 + x2 – 5
⇔ 2x2 + 2x – 2 ≤ 2x2 + 2x – 8
⇔ 6 ≤ 0 (Vô lý).
Vậy BPT vô nghiệm.