Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(x=\dfrac{-2}{7}+\dfrac{9}{7}=1\)
b) \(\dfrac{x}{3}=\dfrac{2}{5}+\dfrac{-4}{3}\)
\(\dfrac{x}{3}=\dfrac{-14}{15}\)
\(\Rightarrow x=\dfrac{3.-14}{15}=\dfrac{-14}{5}\)
\(x=\dfrac{-2}{7}+\dfrac{9}{7}\)
\(x=1\)

a, A= \(5\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\right)\)
\(A=5\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(A=5\left(1-\dfrac{1}{100}\right)\)
\(A=5.\dfrac{99}{100}=\dfrac{99}{20}.\)
b, \(C=1.2.3+2.3.4+...+8.9.10\)
\(4C=1.2.3.4+2.3.4.\left(5-1\right)+...+8.9.10.\left(11-7\right)\)\(4C=1.2.3.4+2.3.4.5-1.2.3.4+...+8.9.10.11-7.8.9.10\)\(4C=8.9.10.11\)
\(C=\dfrac{8.9.10.11}{4}=1980.\)
c, https://hoc24.vn/hoi-dap/question/384591.html
Câu này bạn vào đây mình đã giải câu tương tự nhé.
\(1)A=\dfrac{5}{1.2}+\dfrac{5}{2.3}+...+\dfrac{5}{99.100}\)
\(\Leftrightarrow A=5\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(\Leftrightarrow A=5\left(1-\dfrac{1}{100}\right)\)
\(\Leftrightarrow A=5\cdot\dfrac{99}{100}\)
\(\Leftrightarrow A=\dfrac{99}{20}\)

Ta đặt
\(A=\dfrac{7}{1\times2}+\dfrac{7}{2\times3}+...+\dfrac{7}{99\times100}\)
\(\dfrac{1}{7}\times A=\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+....+\dfrac{1}{99\times100}\)
\(\dfrac{1}{7}\times A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+....+\dfrac{1}{99}-\dfrac{1}{100}\)
\(\dfrac{1}{7}\times A=1-\dfrac{1}{100}\)
\(\dfrac{1}{7}\times A=\dfrac{99}{100}\)
\(A=\dfrac{99}{100}\div\dfrac{1}{7}\)
\(A=\dfrac{693}{100}\)
= 7.(1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + ... + 1/99 - 1/100)
= 7.(1 - 1/100)
= 7 . 99/100
= 693/100

a)\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\frac{1}{9.11}\)
\(=\frac{1}{2}.\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+\frac{2}{9.11}\right)\)
\(=\frac{1}{2}.\left(\frac{3-1}{1.3}+\frac{5-3}{3.5}+\frac{7-5}{5.7}+\frac{9-7}{7.9}+\frac{11-9}{9.11}\right)\)
\(=\frac{1}{2}.\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+\frac{1}{9}-\frac{1}{11}\right)\)
\(=\frac{1}{2}.\left(1-\frac{1}{11}\right)\)
\(\frac{10}{22}\)

Ta có :
\(S=\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+..............+\dfrac{3}{40.43}+\dfrac{3}{43.46}\)
\(S=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...............+\dfrac{1}{40}-\dfrac{1}{43}+\dfrac{1}{43}-\dfrac{1}{46}\)
\(S=1-\dfrac{1}{46}< 1\)
\(\Rightarrow S< 1\rightarrowđpcm\)
\(S=\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{40.43}+\dfrac{3}{43.46}\)
\(S=\dfrac{1}{1.4}+\dfrac{1}{4.7}+\dfrac{1}{7.10}+...+\dfrac{1}{40.43}+\dfrac{1}{43.46}\)
\(S=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{40}-\dfrac{1}{43}+\dfrac{1}{43}-\dfrac{1}{46}\)
\(S=1-\dfrac{1}{46}=\dfrac{45}{46}\)
\(\dfrac{45}{46}< 1\)
=> \(S< 1\)
Tìm x
\(\dfrac{2}{1\cdot4}x+\dfrac{2}{4\cdot7}x+\dfrac{2}{7\cdot10}x+....+\dfrac{2}{31\cdot34}x=10\)

\(\dfrac{2}{1.4}x+\dfrac{2}{4.7}x+\dfrac{2}{7.10}x+...+\dfrac{2}{31.34}x=10\)
\(=>1,5.\left(\dfrac{2}{1.4}x+\dfrac{2}{4.7}x+\dfrac{2}{7.10}x+...+\dfrac{2}{31.34}x\right)=15\)
\(=>\dfrac{3}{1.4}x+\dfrac{3}{4.7}x+\dfrac{3}{7.10}x+...+\dfrac{3}{31.34}x=15\)
\(=>x\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{31.34}\right)=15\)
\(=>x\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{31}-\dfrac{1}{34}\right)=15\)
\(=>x\left(1-\dfrac{1}{34}\right)=15\)
\(=>\dfrac{33}{34}x=15\)
\(=>x=\dfrac{170}{11}\)

\(a,\dfrac{x}{7}=\dfrac{6}{12}\\ x\cdot12=7\cdot6=42\\ x=42:12\\ x=\dfrac{7}{2}\\ b,\dfrac{-5}{x}=\dfrac{20}{28}\\ x\cdot20=\left(-5\right)\cdot28=-140\\ x=\left(-140\right):20\\ x=-7\\ c,\dfrac{x-2}{8}=\dfrac{3}{4}\\ \left(x-2\right)4=8\cdot3=24\\ x-2=24:4\\ x-2=6\\ x=6+2\\ x=8\\ d,\dfrac{x}{-5}=\dfrac{-5}{x}\\ x^2=\left(-5\right)\cdot\left(-5\right)=25\\ x=5\)

\(C=\dfrac{-5}{7}+\dfrac{-2}{7}+\dfrac{3}{4}+\dfrac{1}{4}+\dfrac{-1}{5}=-1+1-\dfrac{1}{5}=\dfrac{-1}{5}\)
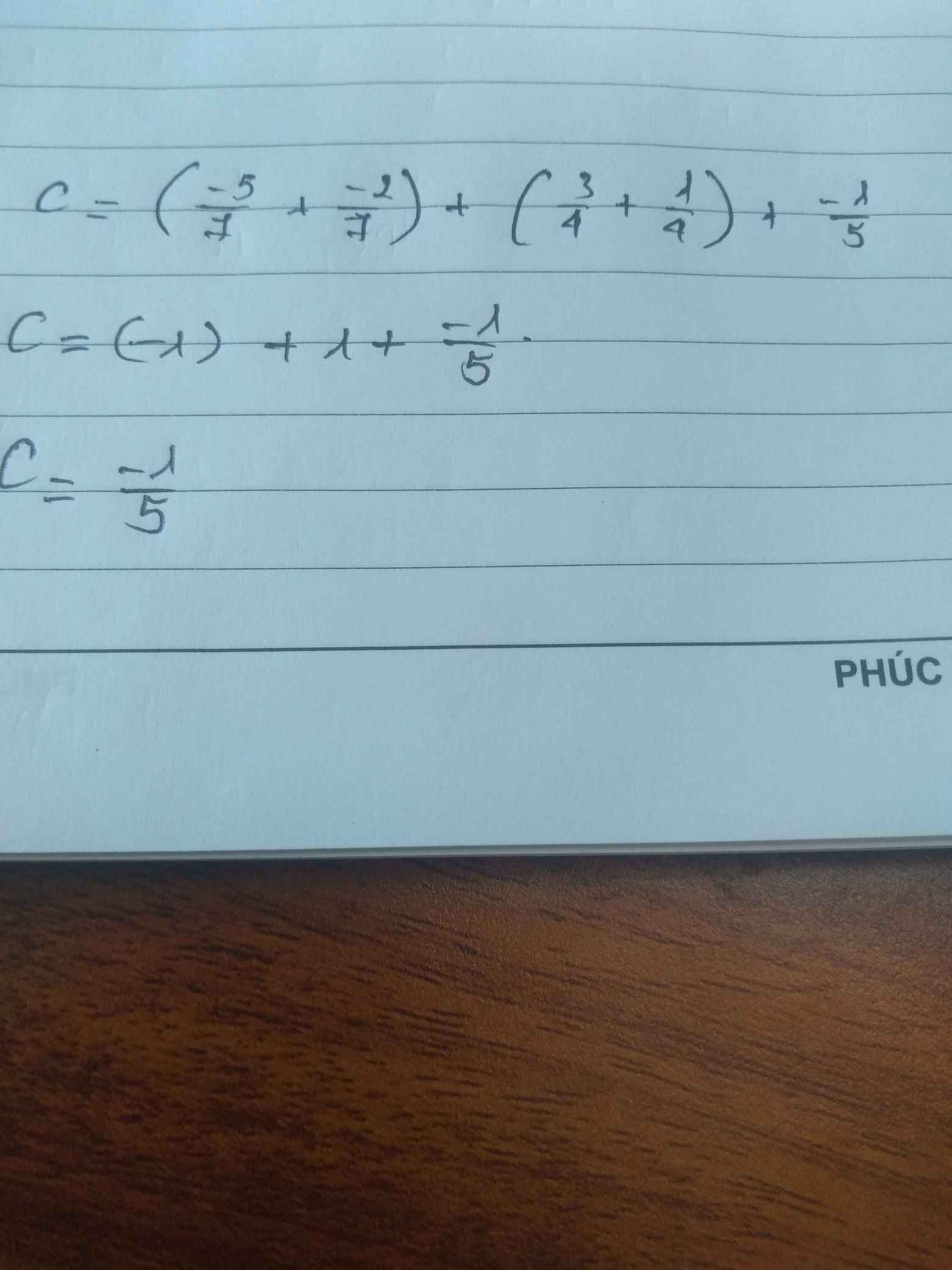
\(\dfrac{x+5}{2005}+\dfrac{x+6}{2004}+\dfrac{x+7}{2003}=-3\\ \Rightarrow\dfrac{x+5}{2005}+1+\dfrac{x+6}{2004}+1+\dfrac{x+7}{2003}+1=0\\ \Rightarrow\dfrac{x+2010}{2005}+\dfrac{x+2010}{2004}+\dfrac{x+2010}{2003}=0\\ \Rightarrow\left(x+2010\right)\left(\dfrac{1}{2005}+\dfrac{1}{2004}+\dfrac{1}{2003}\right)=0\\ \Rightarrow x+2010=0\\ \Rightarrow x=-2010\)
b) \(A=\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{94.97}+\dfrac{3}{97.100}\\ =1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{94}-\dfrac{1}{97}+\dfrac{1}{97}-\dfrac{1}{100}\\ =1-\dfrac{1}{100}=\dfrac{99}{100}\)