Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left(3-m\right)^2=2\left|m-1\right|\)
\(\Leftrightarrow9-6m+m^2=2\left|m-1\right|\left(1\right)\)
TH1: \(m>1\)
\(\left(1\right)\Leftrightarrow9-6m+m^2=2m-2\)
\(\Leftrightarrow m^2-8m+11=0\)
\(\Leftrightarrow\left(m-4\right)^2=5\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4+\sqrt{5}\left(tm\right)\\m=4-\sqrt{5}\left(tm\right)\end{matrix}\right.\)
TH2: \(m< 1\)
\(\left(1\right)\Leftrightarrow9-6m+m^2=2-2m\)
\(\Leftrightarrow m^2-4m+7=0\)
\(\Leftrightarrow\left(m-2\right)^2=-3\)
\(\Rightarrow\text{vô nghiệm}\)
Vậy pt đã cho có 2 nghiệm ...

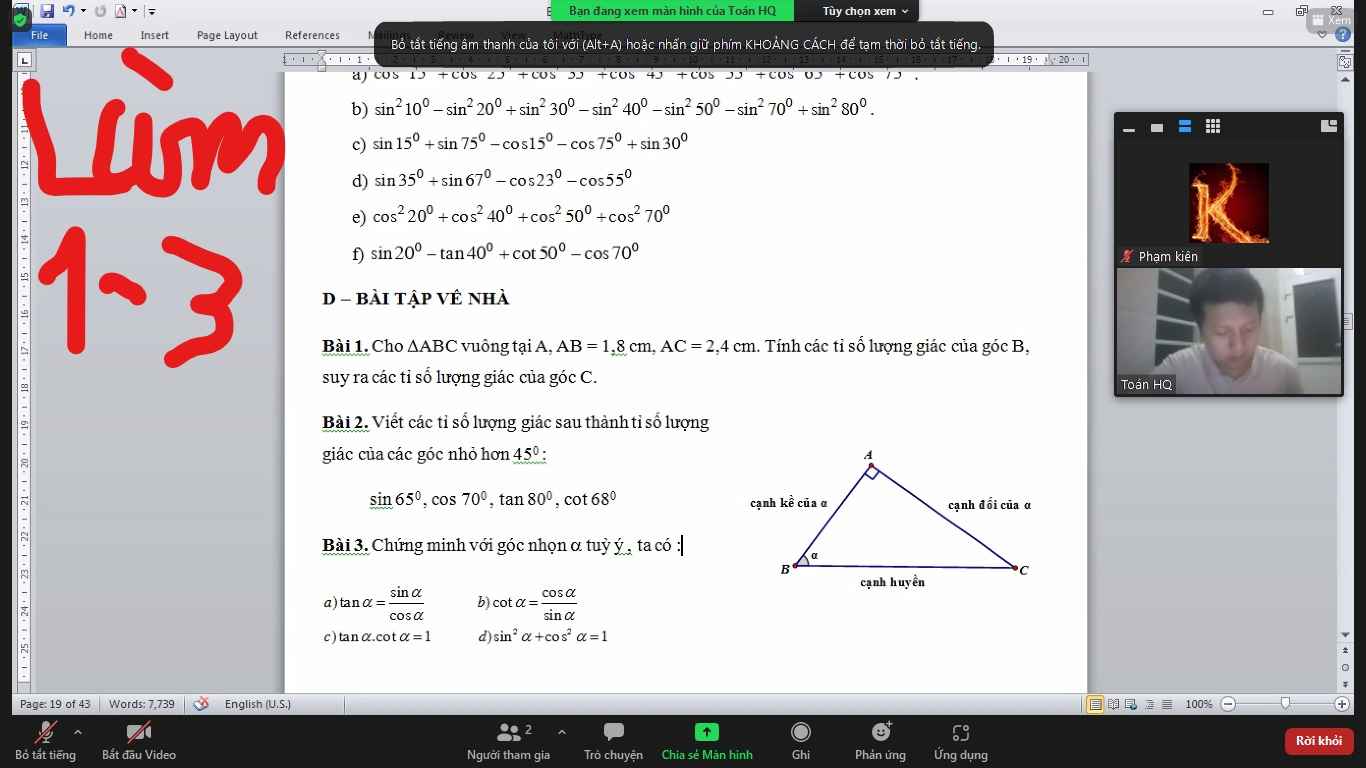
sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)

ĐKXĐ: ...
\(\Leftrightarrow\left(\frac{x^2}{x+1}\right)^2+\frac{x^2}{x+1}-12=0\)
Đặt \(\frac{x^2}{x+1}=t\)
\(\Rightarrow t^2+t-12=0\Rightarrow\left[{}\begin{matrix}t=3\\t=-4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\frac{x^2}{x+1}=3\\\frac{x^2}{x+1}=-4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-3=0\\x^2+4x+4=0\end{matrix}\right.\) \(\Rightarrow\) bấm casio

Lời giải:
ĐKXĐ: $m\neq \frac{1}{2}$
Từ PT $\sqrt{2}-1=\frac{3-m}{2m-1}\Rightarrow (\sqrt{2}-1)(2m-1)=3-m$
$\Leftrightarrow 2+\sqrt{2}=m(2\sqrt{2}-1)$
$\Leftrightarrow m=\frac{2+\sqrt{2}}{2\sqrt{2}-1}=\frac{6+5\sqrt{2}}{7}$ (thỏa mãn)
Vậy...

(\(\sqrt{1+x}+\sqrt{1-x}\))\(\left(2+2\sqrt{1-x^2}\right)=8\)(1)(đk: \(-1\le x\le1\))
đặt \(\sqrt{1+x}+\sqrt{1-x}\) =a (\(a\ge0\)
=> \(a^2=2+2\sqrt{1-x^2}\)
khi đó
(1)\(\Leftrightarrow a^3=8\Leftrightarrow a=\sqrt{8}=2\) (tm)
=>\(\sqrt{1+x}+\sqrt{1-x}\) =2
\(\Leftrightarrow2+2\sqrt{1-x^2}=4\)
\(\Leftrightarrow2\sqrt{1-x^2}=2\)
\(\Leftrightarrow\sqrt{1-x^2}=1\Leftrightarrow1-x^2=1\)
\(\Leftrightarrow x^2=0\Leftrightarrow x=0\)(tm)
vậy x=0 là nghiệm của phương trình
đk: m ≠ 2
TH2 : m < 2 => 2-m > 0
\(3=\frac{9}{2\left|2-m\right|}\)
(=) \(3=\frac{9}{2\left(2-m\right)}\)
(=) 6(2-m) = 9
(=)2-m = 1,5
(=) m = 0,5
TH1 m > 2 => 2-m < 0
\(3=\frac{9}{-2\left(2-m\right)}\)
(=) -6(2-m) = 9
(=) 2-m = -1,5
(=) m = 3,5