K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
3 tháng 1 2019
cos 2 x - sin x - 1 = 0 ⇔ 1 - 2 sin 2 x - sin x - 1 = 0 ⇔ sin x ( 2 sin x + 1 ) = 0
PT
1
CM
22 tháng 10 2019
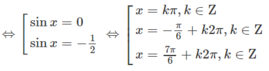
1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0 ( 1 ) T a c ó : 1 - sin 2 x = sin x - cos x 2 ⇔ 2 cos 2 x = 2 ( cos 2 x - sin 2 x ) = - 2 ( sin x - cos x ) ( sin x + cos x ) V ậ y ( 1 ) ⇔ ( sin x - cos x ) ( 1 + sin x - cos x - 2 sin x - 2 cos x ) = 0 ⇔ ( sin x - cos x ) ( 1 - sin x - 3 cos x ) = 0
NH
2
M
19 tháng 8 2023
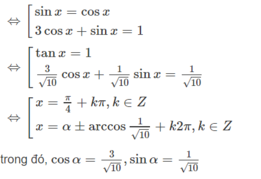
Để giải phương trình cos(2x) - sin(x) = 0, ta có thể sử dụng các công thức lượng giác để đưa phương trình về dạng phù hợp.
Bước 1: Sử dụng công thức cos(2x) = 2cos^2(x) - 1, phương trình trở thành 2cos^2(x) - 1 - sin(x) = 0.
Bước 2: Sử dụng công thức sin^2(x) + cos^2(x) = 1, ta có thể thay thế cos^2(x) bằng 1 - sin^2(x), phương trình trở thành 2(1 - sin^2(x)) - 1 - sin(x) = 0.
Bước 3: Giải phương trình 2 - 2sin^2(x) - 1 - sin(x) = 0.
Bước 4: Đặt sin(x) = t, phương trình trở thành 2 - 2t^2 - 1 - t = 0.
Bước 5: Rút gọn phương trình, ta có -2t^2 - t + 1 = 0.
Bước 6: Giải phương trình bậc hai trên, ta có thể sử dụng công thức hoặc phân tích thành nhân tử để tìm giá trị của t.
Bước 7: Giải phương trình -2t^2 - t + 1 = 0, ta tìm được hai giá trị t = -1 và t = 1/2.
Bước 8: Đặt sin(x) = -1 và sin(x) = 1/2, ta tìm được hai giá trị x = -π/2 và x = π/6.
Vậy, phương trình cos(2x) - sin(x) = 0 có hai nghiệm là x = -π/2 và x = π/6.
19 tháng 8 2023
ĐKXĐ: 1-sin x<>0
=>sin x<>1
=>x<>pi/2+k2pi
cos2x/1-sinx=0
=>cos2x=0
=>2x=pi/2+kpi
=>x=pi/2+kpi/2
Kết hợp ĐKXĐ, ta được: \(x\in\left\{pi+k2pi;\dfrac{3}{2}pi+k2pi;2pi+k2pi\right\}\)
A
1
HP
15 tháng 8 2021
ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{k\pi}{2}\)
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}=0\)
\(\Leftrightarrow2sin^2x+cos4x-cos2x=0\)
\(\Leftrightarrow2sin^2x-1+cos4x-cos2x+1=0\)
\(\Leftrightarrow2cos^22x-2cos2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=k\pi\end{matrix}\right.\)
Đối chiếu điều kiện ta được \(x=-\dfrac{\pi}{4}+k\pi\)
MA
1
30 tháng 6 2021
a)Đk:\(sinx\ne1\)
Pt\(\Leftrightarrow sin^2x+sinx=-2\left(sinx-1\right)\)
\(\Leftrightarrow sin^2x+3sinx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{-3+\sqrt{17}}{2}\left(tm\right)\\sinx=\dfrac{-3-\sqrt{17}}{2}\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\\x=\pi-arc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\end{matrix}\right.\)(\(k\in Z\))
b)Đk:\(sinx\ne1\)
Pt \(\Leftrightarrow\dfrac{1-2sin^2x+sinx}{sinx-1}+1=0\)
\(\Leftrightarrow\dfrac{-\left(sinx-1\right)\left(2sinx+1\right)}{sinx-1}+1=0\)
\(\Leftrightarrow-\left(2sinx+1\right)+1=0\)
\(\Leftrightarrow sinx=0\) (tm)
\(\Leftrightarrow x=k\pi,k\in Z\)
Vậy...
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
\(\begin{array}{l}a)\;sin2x + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) = - cos3x\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) = cos\left( {\pi - 3x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{2} - 2x = \pi - 3x + k2\pi \\\frac{\pi }{2} - 2x = - \pi + 3x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{{3\pi }}{{10}} + k\frac{{2\pi }}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}b)\;sinx.cosx = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow \frac{1}{2}\;sin2x = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow sin2x = \frac{{\sqrt 2 }}{2} = sin\left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{4} + k2\pi \\2x = \pi - \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{8} + k\pi \\x = \frac{{3\pi }}{8} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}c)\;sinx + sin2x = 0\\ \Leftrightarrow sinx = - sin2x\\ \Leftrightarrow sinx = sin( - 2x)\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2x + k2\pi \\x = \pi + 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\frac{{2\pi }}{3}\\x = - \pi + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
DH
1
HP
17 tháng 10 2021
ĐK: \(x\ne\dfrac{\pi}{6}+k2\pi;x\ne\dfrac{5\pi}{6}+k2\pi\)
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=0\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=0\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
Đối chiếu điều kiện ta được \(x=-\dfrac{5\pi}{6}+k2\pi\).
PT
1
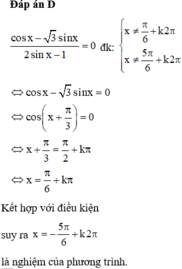
Điều kiện x ≠ kπ ∀ k ∈ Z
Vậy phương trình có tập nghiệm