K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
25 tháng 4 2017
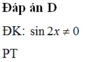
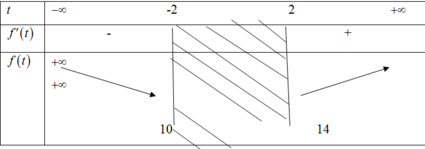
Do đó phương trình có nghiệm khi
Vậy số giá trị nguyên của α
nhỏ hơn 2018 thỏa mãn yêu cầu
đề bài là 
TA
9 tháng 10 2022
a) cos3x = \(cos\left(\pi-x-\dfrac{\pi}{3}\right)\)
<=> cos3x = \(cos\left(\dfrac{2\pi}{3}-x\right)\)
<=> 3x = \(\dfrac{2\pi}{3}-x\) hoặc 3x = \(\dfrac{-2\pi}{3}+x\)
<=> 4x = \(\dfrac{2\pi}{3}+k2\pi\) hoặc 2x = \(\dfrac{-2\pi}{3}+k2\pi\)
<=> x = \(\dfrac{\pi}{6}+\dfrac{k\pi}{2}\) hoặc x = \(\dfrac{-\pi}{3}+k\pi\)
<=> x = \(\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{2};\dfrac{-\pi}{3}+k\pi;k\in Z\right\}\)
b ) Điều kiện sinx\(\ne0;cosx\ne0\)
<=> sin2x\(\ne0\) <=> x \(\ne\dfrac{k\pi}{2}\);k\(\in Z\)
tanx + cotx =0
<=> tan2x + tanx =0
<=> tanx(tanx+1)=0
<=> tanx=0 hoặc tanx = -1
<=> x=\(k\pi\) (loại) hoặc x = \(\dfrac{-\pi}{4}+k\pi\)
Vậy x = \(\dfrac{-\pi}{4}+k\pi;k\in Z\)
CM
26 tháng 9 2019
Điều kiện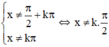 
tanx – 2.cotx + 1 = 0
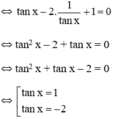
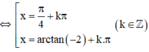(Thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm
{
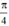+ kπ; arctan(-2) + kπ} (k ∈ Z)
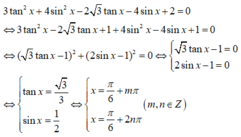
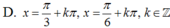
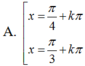
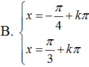
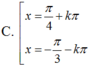
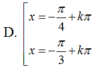
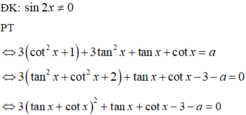
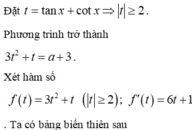
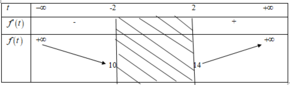
3tan2 x - 2√3 tanx + 3 = 0
Đặt tanx = t
ta được phương trình bậc hai theo t:
3t2 - 2√3 t + 3 = 0(1)
Δ = (-2√3)2 - 4.3.3 = -24 < 0
Vậy Phương trình (1) vô nghiệm, nên không có x thỏa mãn đề bài