Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(x^2+xy+y^2+1\)
\(=x^2+xy+\dfrac{y^2}{4}-\dfrac{y^2}{4}+y^2+1\)
\(=\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1\)
mà \(\left\{{}\begin{matrix}\left(x+\dfrac{y}{2}\right)^2\ge0,\forall x;y\\\dfrac{3y^2}{4}\ge0,\forall x;y\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1>0,\forall x;y\)
\(\Rightarrow dpcm\)
b) \(...=x^2-2x+1+4\left(y^2+2y+1\right)+z^2-6z+9+1\)
\(=\left(x-1\right)^2+4\left(y^{ }+1\right)^2+\left(z-3\right)^2+1>0,\forall x.y\)
\(\Rightarrow dpcm\)

Bài 1. x^2 \(\equiv\)8 (mod 0,1). (cmdd)
T tự: y^2 \(\equiv\)8 (mod 0,1)
=> x^2+y^2 \(\equiv\)8 (mod 0,1,2)
Mà 8z+6 \(\equiv\)8 (mod 6)
=> đpcm

a, TK: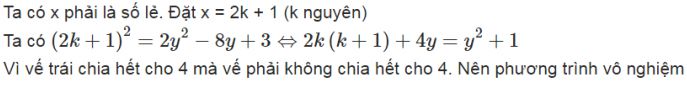
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương

\(\Leftrightarrow4y^2=4x^4+4x^3+4x^2+4x+4\)
Ta có:
\(4x^4+4x^3+4x^2+4x+4=\left(2x^2+x\right)^2+2x^2+\left(x+2\right)^2>\left(2x^2+x\right)^2\)
\(4x^4+4x^3+4x^2+4x+4=\left(2x^2+x+2\right)^2-5x^2\le\left(2x^2+x+2\right)^2\)
\(\Rightarrow\left(2x^2+x\right)^2< \left(2y\right)^2\le\left(2x^2+x+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}\left(2y\right)^2=\left(2x^2+x+1\right)^2\\\left(2y\right)^2=\left(2x^2+x+2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}4x^4+4x^3+4x^2+4x+4=\left(2x^2+x+1\right)^2\\4x^4+4x^3+4x^2+4x+4=\left(2x^2+x+2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-2x-3=0\\5x^2=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=3\end{matrix}\right.\)
- Với \(x=0\Rightarrow y^2=1\Rightarrow y=\pm1\)
- Với \(x=-1\Rightarrow y^2=1\Rightarrow y=\pm1\)
- Với \(x=3\Rightarrow y^2=121\Rightarrow y=\pm11\)

\(=x^2y-x^2z+y^2\left(z-x\right)+xz^2-yz^2\\ =\left(x^2y-yz^2\right)-\left(x^2z-xz^2\right)-y^2\left(x-z\right)\\ =y\left(x-z\right)\left(x+z\right)-xz\left(x-z\right)-y^2\left(x-z\right)\\ =\left(x-z\right)\left(xy+yz-xz-y^2\right)\\ =\left(x-z\right)\left[x\left(y-z\right)+y\left(z-y\right)\right]\\ =\left(x-y\right)\left(y-z\right)\left(x-z\right)\)

a) \(\frac{-x^2y^5}{-x^2y^5}=1\)
b)\(\frac{-\left(x^7y^5z\right)^2}{-\left(xy^3z\right)^2}=\frac{x^{14}y^{10}z^2}{x^2y^6z^2}=x^7.y^4\)Thế vào ta được 1.(-10)^4=10000 cái khi nãy làm lộn
câu a cả tử và mẫu đều giống nhau nên kết quả là 1
b) chia ra ta được x6y2. Thế vào thì ra 1.102=100