LT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BT
0
25 tháng 12 2021
\(a,PT\Leftrightarrow\left(1-2m\right)x=m+4\)
Bậc nhất \(\Leftrightarrow1-2m\ne0\Leftrightarrow m\ne\dfrac{1}{2}\)
\(b,x=2\Leftrightarrow2-4m-m-4=0\Leftrightarrow m=-\dfrac{2}{5}\\ c,m=5\Leftrightarrow-9x-9=0\Leftrightarrow x=-1\)
27 tháng 2 2023
a: Để đây là phương trình bậc nhất một ẩn thì 2m+1<>0
=>m<>-1/2
b: 2x+3=4
=>x=1/2
Thay x=1/2 vào (1), ta đc:
1/2(2m+1)+2m-3=0
=>m+1/2+2m-3=0
=>3m-5/2=0
=>m=5/6
15 tháng 1 2022
Để phương trình trên là phương trình bậc nhất 1 ẩn thì
\(\left(2m+3\right)\left(1-m\right)\left(x-m\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2m+3=0\\1-m=0\\x-m=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=1\\m=x\end{matrix}\right.\)
VL
24 tháng 1 2021
a. m2 ≥ 0 ∀ m
=> m2 +1> 0 ∀ m
b. m2 +2m +3 = m2 + 2m +1 +2 = (m + 1)2 + 2 > 0 ∀ m
c. m2 ≥ 0 ∀ m
=> m2 +2> 0 ∀ m
d. m2 - 2m +2 = m2 -2m + 1 +1 = (m - 1)2 + 1 > 0 ∀ m
24 tháng 1 2021
a) Để phương trình \(\left(m^2+1\right)x-3=0\) là phương trình bậc nhất một ẩn thì \(m^2+1\ne0\)
\(\Leftrightarrow m^2\ne-1\)
mà \(m^2\ge0\forall m\)
nên \(m^2\ne-1\forall m\)
\(\Leftrightarrow m^2+1\ne0\forall m\)
Vậy: Phương trình \(\left(m^2+1\right)x-3=0\) là phương trình bậc nhất một ẩn với mọi giá trị của tham số m
b) Để phương trình \(\left(m^2+2m+3\right)x+m-1=0\) là phương trình bậc nhất một ẩn thì \(m^2+2m+3\ne0\)
\(\Leftrightarrow\left(m+1\right)^2+2\ne0\)
mà \(\left(m+1\right)^2+2\ge2>0\forall m\)
nên \(\left(m+1\right)^2+2\ne0\forall m\)
hay \(m^2+2m+3\ne0\forall m\)
Vậy: Phương trình \(\left(m^2+2m+3\right)x+m-1=0\) luôn là phương trình bậc nhất một ẩn với mọi tham số m
c) Để phương trình \(\left(m^2+2\right)x-4=0\) là phương trình bậc nhất một ẩn thì \(m^2+2\ne0\)
\(\Leftrightarrow m^2\ne-2\)
mà \(m^2\ge0\forall m\)
nên \(m^2\ne-2\forall m\)
\(\Leftrightarrow m^2+2\ne0\forall m\)
Vậy: Phương trình \(\left(m^2+2\right)x+4=0\) là phương trình bậc nhất một ẩn với mọi giá trị của tham số m
d) Để phương trình \(\left(m^2-2m+2\right)x+m=0\) là phương trình bậc nhất một ẩn thì \(m^2-2m+2\ne0\)
\(\Leftrightarrow\left(m-1\right)^2+1\ne0\)
mà \(\left(m-1\right)^2+1\ge1>0\forall m\)
nên \(\left(m-1\right)^2+1\ne0\forall m\)
hay \(m^2-2m+2\ne0\forall m\)
Vậy: Phương trình \(\left(m^2-2m+2\right)x+m=0\) luôn là phương trình bậc nhất một ẩn với mọi tham số m
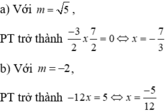
Lời giải:
PT $\Leftrightarrow x^2-x(2m+1)+m(2m+1)=0$
$\Delta=(2m+1)^2-4m(2m+1)=(2m+1)(1-2m)$
Nếu $\frac{-1}{2}< m< \frac{1}{2}$ thì $\Delta>0$
PT có 2 nghiệm phân biệt \(\left\{\begin{matrix} x_1=\frac{2m+1+\sqrt{(2m+1)(1-2m)}}{2}\\ x_2=\frac{2m+1-\sqrt{(2m+1)(1-2m)}}{2}\end{matrix}\right.\)
Nếu $m=\frac{-1}{2}\Rightarrow \Delta=0$. PT có nghiệm kép $x_1=x_2=\frac{2m+1}{2}=0$
Nếu $m=\frac{1}{2}\Rightarrow \Delta=0$. PT có nghiệm kép $x_1=x_2=\frac{2m+1}{2}=1$
Nếu $m< \frac{-1}{2}$ hoặc $m> \frac{1}{2}$ thì $\Delta< 0$: PT vô nghiệm
Lời giải:
PT $\Leftrightarrow x^2-x(2m+1)+m(2m+1)=0$
$\Delta=(2m+1)^2-4m(2m+1)=(2m+1)(1-2m)$
Nếu $\frac{-1}{2}< m< \frac{1}{2}$ thì $\Delta>0$
PT có 2 nghiệm phân biệt \(\left\{\begin{matrix} x_1=\frac{2m+1+\sqrt{(2m+1)(1-2m)}}{2}\\ x_2=\frac{2m+1-\sqrt{(2m+1)(1-2m)}}{2}\end{matrix}\right.\)
Nếu $m=\frac{-1}{2}\Rightarrow \Delta=0$. PT có nghiệm kép $x_1=x_2=\frac{2m+1}{2}=0$
Nếu $m=\frac{1}{2}\Rightarrow \Delta=0$. PT có nghiệm kép $x_1=x_2=\frac{2m+1}{2}=1$
Nếu $m< \frac{-1}{2}$ hoặc $m> \frac{1}{2}$ thì $\Delta< 0$: PT vô nghiệm