K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 2 2021
\(a,2x\left(x-5\right)+4\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(2x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\2x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\2x=-4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
Vậy \(x\in\left\{5;-2\right\}\)
\(b,3x-15=2x\left(x-5\right)\\ \Leftrightarrow3\left(x-5\right)-2x\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(-2x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\-2x+3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\2x=3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{5;\dfrac{3}{2}\right\}\)
\(c,\left(2x+1\right)\left(3x-2\right)=\left(5x-8\right)\left(2x+1\right)\\ \Leftrightarrow\left(2x+1\right)\left(3x-2\right)-\left(5x-8\right)\left(2x+1\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(3x-2-5x+8\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(-2x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x+1=0\\-2x+6=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=-1\\2x=6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Vậy \(x\in\left\{-\dfrac{1}{2};3\right\}\)
Câu d xem lại đề
PT
1
CM
17 tháng 11 2017
Điều kiện xác định: x ≠ 1; x ≠ 2; x ≠ 3.
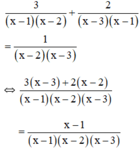
⇒ 3(x – 3) + 2(x – 2) = x – 1
⇔ 3x – 9 + 2x – 4 = x – 1
⇔ 3x + 2x – x = 9 + 4 – 1
⇔ 4x = 12
⇔ x = 3 (không thỏa mãn điều kiện xác định)
Vậy phương trình vô nghiệm.
6 tháng 2 2022
a: =>3x=-9
hay x=-3
b: =>3x=2
hay x=2/3
c: =>2x=4
hay x=2
d: =>-2x=-6
hay x=3
e: =>0,5x=1
hay x=2
f: =>0,6x=3,6
hay x=6
g: =>2/3x=4/3
hay x=2
h: =>-3x+3=6x+2
=>-9x=-1
hay x=1/9
i: =>4x-2x=1+3
=>2x=4
hay x=2
HP
6 tháng 2 2022
\(A.3x+9=0\)
\(\Leftrightarrow3x=-9\)
\(\Leftrightarrow x=-2\)
\(B.3x-2=0\)
\(\Leftrightarrow3x=2\)
\(\Leftrightarrow x=\dfrac{2}{3}\)
\(C.4-2x=0\)
\(\Leftrightarrow4=2x\)
\(\Leftrightarrow x=2\)
\(D.-2x+6=0\)
\(\Leftrightarrow6=2x\)
\(\Leftrightarrow x=3\)
\(E.0,5x-1=0\)
\(\Leftrightarrow0,5x=1\)
\(\Leftrightarrow x=2\)
\(F.3,6-0,6x=0\)
\(\Leftrightarrow3,6=0,6x\)
\(\Leftrightarrow x=6\)
\(G.\dfrac{2}{3}x-1=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{2}{3}x=\dfrac{4}{3}\)
\(\Leftrightarrow x=2\)
\(H.-\dfrac{1}{3}x+1=\dfrac{2}{3}x-3\)
\(\Leftrightarrow4=x\)
\(\Leftrightarrow x=4\)
\(I.4x-3=2x+1\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\)
CM
18 tháng 3 2019
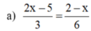
⇔ 4x - 10 = 2 - x
⇔ 4x + x = 2 + 10 ⇔ 5x = 12 ⇔ x = 12/5
Vậy: S = {12/5}
b) (3x + 1) = (3x + 1)2
⇔ (3x + 1)2 - (3x + 1) = 0
⇔ (3x + 1)[(3x + 1) - 1] = 0
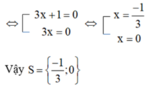
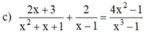
ĐKXĐ:x ≠ 1
Quy đồng mẫu hai vế của phương trình ta được:
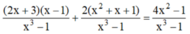
Khử mẫu hai vế, ta được:
(2x + 3)(x - 1) + 2(x2 + x + 1) = 4x2 - 1
⇔ 2x2 + x - 3 + 2x2 + 2x + 2 = 4x2 - 1
⇔ 3x - 1 = -1
⇔ 3x = 0 ⇔ x = 0 (thỏa mãn điều kiện)
Vậy: S = {0}
BC
1
16 tháng 1 2021
\(\left(x-1\right)^3-\left(x-1\right)\left(2x-3\right)\left(3x-5\right)+\left(2x-3\right)^3-\left(x-1\right)\left(2x-3\right)\left(3x-5\right)+\left(3x-5\right)^3-\left(x-1\right)\left(2x-3\right)\left(3x-5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(\left(x-1\right)^2-\left(2x-3\right)\left(3x-5\right)\right)+\left(2x-3\right)\left(\left(2x-3\right)^2-\left(x-1\right)\left(3x-5\right)\right)+\left(3x-5\right)\left(\left(3x-5\right)^2-\left(x-1\right)\left(2x-3\right)\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(7-5x\right)+\left(2x-3\right)\left(x-2\right)^2+\left(3x-5\right)\left(x-2\right)\left(7x-11\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(\left(x-1\right)\left(7-5x\right)+\left(2x-3\right)\left(x-2\right)+\left(3x-5\right)\left(7x-11\right)\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(18x^2-63x+54\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\18x^2-63x+54=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{3}{2}\end{matrix}\right.\)
CM
3 tháng 11 2017
Hướng dẫn:
Ta có 2x - ( 3 - 2x ) = 3x + 1 ⇔ 2x - 3 + 2x = 3x + 1
⇔ 4x - 3x = 1 + 3 ⇔ x = 4.
Vậy phương trình đã cho có tập nghiệm là S = { 4 }.
CM
14 tháng 2 2018
(2x + 1)(3x – 2) = (5x – 8)(2x + 1)
⇔ (2x + 1)(3x – 2) – (5x – 8)(2x + 1) = 0
⇔ (2x + 1).[(3x – 2) – (5x – 8)] = 0
⇔ (2x + 1).(3x – 2 – 5x + 8) = 0
⇔ (2x + 1)(6 – 2x) = 0
⇔ 2x + 1 = 0 hoặc 6 – 2x = 0
+ 2x + 1 = 0 ⇔ 2x = -1 ⇔ x = -1/2.
+ 6 – 2x = 0 ⇔ 6 = 2x ⇔ x = 3.
Vậy phương trình có tập nghiệm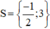 
12 tháng 8 2021
1/ ( x-1) (2x+1) =0
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\2x+1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-0,5\end{matrix}\right.\)
2/ x (2x-1) (3x+15) =0
\(\Rightarrow\left[{}\begin{matrix}x=0\\2x-1=0\\3x+15=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=0,5\\x=-5\end{matrix}\right.\)
3/ (2x-6) (3x+4).x=0
\(\Rightarrow\left[{}\begin{matrix}2x-6=0\\3x+4=0\\x=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{4}{3}\\x=0\end{matrix}\right.\)
4/ (2x-10)(x2+1)=0
\(\Rightarrow\left[{}\begin{matrix}2x-10=0\\x^2+1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\x^2=-1\left(loại\right)\end{matrix}\right.\)
5/ (x2+3) (2x-1) =0
\(\Rightarrow\left[{}\begin{matrix}x^2+3=0\\2x-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x^2=-3\left(loại\right)\\x=0,5\end{matrix}\right.\)
6/ (3x-1) (2x2 +1)=0
\(\Rightarrow\left[{}\begin{matrix}3x-1=0\\2x^2+1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x^2=-0,5\left(loại\right)\end{matrix}\right.\)
12 tháng 8 2021
1: Ta có: \(\left(x-1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{2}\end{matrix}\right.\)
2: Ta có: \(x\left(2x-1\right)\left(3x+15\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2x-1=0\\3x+15=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=-5\end{matrix}\right.\)
3: Ta có: \(\left(2x-6\right)\left(3x+4\right)x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-6=0\\3x+4=0\\x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{4}{3}\\x=0\end{matrix}\right.\)
AT
1
Y
9 tháng 3 2023
\(a,6x^2-5x+3=2x-3x\left(3-2x\right)\)
\(\Leftrightarrow6x^2-5x+3=2x-9x+6x^2\)
\(\Leftrightarrow6x^2-6x^2-5x-2x+9x=-3\)
\(\Leftrightarrow2x=-3\)
\(\Leftrightarrow x=-\dfrac{3}{2}\)
\(b,\left(3x-1\right)\left(4x+3\right)=2\left(3x-1\right)\)
\(\Leftrightarrow\left(3x-1\right)\left(4x+3\right)-2\left(3x-1\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(4x+3-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\4x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
10 tháng 3 2023
\(6x^2-5x+3=2x-3x\left(3-2x\right)\)
\(\Leftrightarrow6x^2-5x+3=2x-9x+6x^2\)
\(\Leftrightarrow6x^2-5x+3-2x+9x-6x^2=0\)
\(\Leftrightarrow2x+3=0\)
\(\Leftrightarrow2x=-3\)
\(\Leftrightarrow x=\dfrac{-3}{2}\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{\dfrac{-3}{2}\right\}\)
\(\left(3x-1\right)\left(4x+3\right)=2\left(3x-1\right)\)
\(\Leftrightarrow\left(3x-1\right)\left(4x+3\right)-2\left(3x-1\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(4x+3-2\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(4x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\4x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=1\\4x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=\dfrac{1}{4}\end{matrix}\right.\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{\dfrac{1}{3};\dfrac{1}{4}\right\}\)
2x(3x-1) - (3x-1) = 0.
Nhóm 3x-1 ra ngoài ta có
(3x-1)(2x-1) = 0.
Pt trên bằng 0 khi và chỉ khi 1 trong 2 giá trị 3x -1 hoặc 2x-1 =0 => x=1/2 hoặc x=1/3