
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e: \(\Leftrightarrow\left\{{}\begin{matrix}10y=40\\4x+7y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\4x=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=-3\end{matrix}\right.\)
\(d,\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2y+11}{3}\\\dfrac{4\left(2y+11\right)}{3}-5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2y+11}{3}\\8y+44-15y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2y+11}{3}\\-7y=-35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10+11}{3}=7\\y=5\end{matrix}\right.\)
\(e,\Leftrightarrow\left\{{}\begin{matrix}4x=16-7y\\16-7y-3y=-24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=16-7y\\10y=40\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4x=16-7\cdot4=-12\\y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=4\end{matrix}\right.\)

\(g,\Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\x-15y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=15y+16\\30y+32+10y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=15y+8\\40y=-33\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{33}{40}\cdot15+8=\dfrac{29}{8}\\y=-\dfrac{33}{40}\end{matrix}\right.\)
\(h,\Leftrightarrow\left(x-15\right)\left(y+2\right)=\left(x+15\right)\left(y-1\right)\\ \Leftrightarrow xy+2x-15y-30=xy-x+15y-15\\ \Leftrightarrow3x=30y+15\Leftrightarrow x=10y+5\\ \text{Ta có }PT\left(1\right)\Leftrightarrow xy+2x-15y-30=xy\Leftrightarrow2x-15y=30\\ \Leftrightarrow2\left(10y+5\right)-15y=30\\ \Leftrightarrow y=4\Leftrightarrow x=45\)
\(i,\Leftrightarrow\left\{{}\begin{matrix}x=5\sqrt{5}-2y\\\sqrt{5}\left(5\sqrt{5}-2y\right)+y=5+2\sqrt{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5\sqrt{5}-2y\\25-2\sqrt{5}y+y=5+2\sqrt{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5\sqrt{5}-2y\\y\left(1-2\sqrt{5}\right)=20-2\sqrt{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5\sqrt{5}-2y\\y=\dfrac{20-2\sqrt{5}}{1-2\sqrt{5}}=\dfrac{2\sqrt{5}\left(2\sqrt{5}-1\right)}{-\left(2\sqrt{5}-1\right)}=-2\sqrt{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5\sqrt{5}+4\sqrt{5}=9\sqrt{5}\\y=-2\sqrt{5}\end{matrix}\right.\)
Câu i sửa: \(PT\left(2\right)\Leftrightarrow y=5+2\sqrt{5}-\sqrt{5}x\)
Thế vào \(PT\left(1\right)\Leftrightarrow x+10+4\sqrt{5}-2\sqrt{5}x=5\sqrt{5}\)
\(\Leftrightarrow x\left(1-2\sqrt{5}\right)=\sqrt{5}-10\\ \Leftrightarrow x=\dfrac{\sqrt{5}-10}{1-2\sqrt{5}}=\dfrac{\sqrt{5}\left(1-2\sqrt{5}\right)}{1-2\sqrt{5}}=\sqrt{5}\\ \Leftrightarrow y=5+2\sqrt{5}-5=2\sqrt{5}\)

Ta có: \(\left\{{}\begin{matrix}2x-3y=1\\-4x+6y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3y=1\\-2\left(2x-3y\right)=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-3y=1\\2x-3y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1=1\left(vôlý\right)\\2x-3y=1\end{matrix}\right.\)
Vậy: Hệ phương trình vô nghiệm

Ta có: \(\left\{{}\begin{matrix}-x-y=2\\-2x-3y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\left(x+y\right)=2\\-\left(2x+3y\right)=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=-2\\2x+3y=-9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-2-y\\2\cdot\left(-2-y\right)+3y=-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2-y\\-4-2y+3y+9=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-2-y\\y+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2-y\\y=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-2-\left(-5\right)\\y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2+5=3\\y=-5\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=3\\y=-5\end{matrix}\right.\)

\(\hept{\begin{cases}x-y=m\left(1\right)\Rightarrow y=x-m\\2x+y=4\left(2\right)\end{cases}}\)
Thay vào (2) => 2x+(x-m)=4
\(\Leftrightarrow\hept{\begin{cases}y=x-m\\3x-m-4=0\end{cases}\Leftrightarrow\hept{\begin{cases}y=x-m\\x=\frac{4+m}{3}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{4+m}{3}\\y=\frac{4-m}{3}-m=\frac{4-4m}{3}\end{cases}}}\)
\(\hept{\begin{cases}x-y=m\\2x+y=4\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x-y+2x+y=m+4\\2x+y=4\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}3x=m+4\\2x+y=4\end{cases}}\) \(\Leftrightarrow\) \(\hept{\begin{cases}x=\frac{m+4}{3}\\2.\frac{m+4}{3}+y=4\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=\frac{m+4}{3}\\\frac{2m+8}{3}+y=4\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x=\frac{m+4}{3}\\y=\frac{4-2m}{3}\end{cases}}\) Vậy hệ pt có nghiệm duy nhất là: \(\left(x;y\right)=\left(\frac{m+4}{3};\frac{4-2m}{3}\right)\)

Lời giải:
Gọi vận tốc hai người lần lượt là $a$ và $b$ (km/h)
ĐK: $a< b$
Gọi thời gian mà người đi sau đi đến khi gặp người đi trước là $t$ (giờ)
Theo bài ra ta có:
$\frac{a}{b}=\frac{3,6-2}{2}=\frac{4}{5}(1)$
$a(t+\frac{6}{60})=bt=3,6:2=1,8(2)$
Từ $(1);(2)$ ta có hệ:
\(\left\{\begin{matrix} \frac{a}{b}=\frac{4}{5}\\ a(t+\frac{1}{10})=bt=1,8\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=0,8b\\ a(t+\frac{1}{10})=bt=1,8\end{matrix}\right.\)
\(\Leftrightarrow 0,8b(t+\frac{1}{10})=bt=1,8\)
\(\Leftrightarrow \left\{\begin{matrix} 0,08b=0,2bt\\ bt=1,8\end{matrix}\right.\Rightarrow 0,08b=0,2.1,8=0,36\)
\(\Rightarrow b=4,5\) (km/h)
$a=0,8b=3,6$ (km/h)


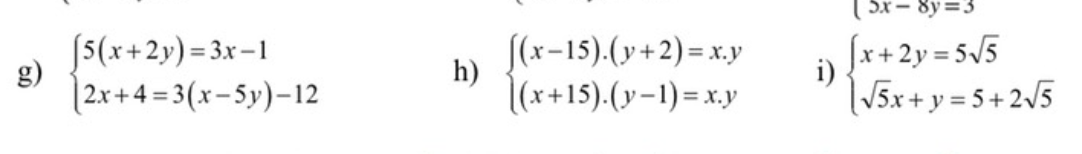
 Lập bảng và giải bằng hpt giúp e ạ
Lập bảng và giải bằng hpt giúp e ạ
d: \(\Leftrightarrow\left\{{}\begin{matrix}12x-8y=44\\12x-15y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\x=7\end{matrix}\right.\)
\(i,\Leftrightarrow\left\{{}\begin{matrix}x+2y=5\sqrt{5}\\2\sqrt{5}x+2y=10+4\sqrt{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left(2\sqrt{5}-1\right)x=10-\sqrt{5}\\x+2y=5\sqrt{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10-\sqrt{5}}{2\sqrt{5}-1}=\dfrac{\sqrt{5}\left(2\sqrt{5}-1\right)}{2\sqrt{5}-1}=\sqrt{5}\\\sqrt{5}+2y=5\sqrt{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{5}\\y=2\sqrt{5}\end{matrix}\right.\)