K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TR
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2022
5.
\(\Delta=\left(-2\right)^2-4\left(-15\right)=64\)
6.
\(\Delta'=2^2-5.\left(-7\right)=39\)
8 tháng 2 2022
Mà thầy ơi em hok hiểu khúc đầu làm sao để ra cái đó ròi ra kết quả á :((( cả 2 câu lun
4 tháng 4 2021
Ta có: \(\Delta=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(m-3\right)\)
\(=\left(2m-2\right)^2-4\left(m-3\right)\)
\(=4m^2-8m+4-4m+12\)
\(=4m^2-12m+16\)
\(=4m^2-2\cdot2m\cdot3+9+7\)
\(=\left(2m-3\right)^2+7>0\forall x\)
Do đó, phương trình luôn có hai nghiệm phân biệt với mọi m
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)=2m-2\\x_1\cdot x_2=m-3\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\\2x_1-3x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=4m-4\\2x_1-3x_2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x_2=4m-4\\x_1=2m-2-x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4m-4}{5}\\x_1=\dfrac{10m-10-4m+4}{5}=\dfrac{6m-6}{5}\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=m-3\)
\(\Leftrightarrow\dfrac{4m-4}{5}\cdot\dfrac{6m-6}{5}=m-3\)
\(\Leftrightarrow\left(4m-4\right)\left(6m-6\right)=25\left(m-3\right)\)
\(\Leftrightarrow24m^2-24m-24m+24=25m-75\)
\(\Leftrightarrow24m^2-48m+24-25m+75=0\)
\(\Leftrightarrow24m^2-73m+99=0\)(1)
\(\Delta=\left(-73\right)^2-4\cdot24\cdot99=-4175< 0\)
Suy ra: Phương trình (1) vô nghiệm
Vậy: Không có giá trị nào của m để phương trình \(x^2-2\left(m-1\right)x+m-3=0\) có hai nghiệm phân biệt thỏa mãn \(2x_1-3x_2=0\)
MN
12 tháng 7 2021
Áp dụng hệ thức lượng trong tam giác vuông ABC :
\(AB^2=HB\cdot BC\)
\(\Leftrightarrow AB^2=HB\cdot\left(HB+HC\right)\)
\(\Leftrightarrow3^2=HB^2+3.2HB\)
\(\Leftrightarrow HB^2+3.2HB-9=0\)
\(\Leftrightarrow\left[{}\begin{matrix}HB=1.8\left(N\right)\\HB=-5\left(L\right)\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
Ta có: \(BH+HC=BC\Rightarrow BC=BH+3,2\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\)
\(\Leftrightarrow3^2=BH.\left(BH+3,2\right)\)
\(\Leftrightarrow BH^2+3,2BH-9=0\) (bấm máy phương trình bậc 2: \(x^2+3,2x-9=0\))
\(\Rightarrow\left[{}\begin{matrix}BH=-5< 0\left(loại\right)\\BH=1,8\end{matrix}\right.\)
Vậy \(BH=1,8\left(cm\right)\)
29 tháng 6 2021
1, \(P=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right).\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}.\left(\sqrt{x}+1\right)\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
b, Ta có : \(x^2-3x+2=x^2-2x-x+2=x\left(x-2\right)-\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
TH1 : Thay x = 1 vào biểu thức P ta được : \(P=\dfrac{1+\sqrt{1}+1}{1}=3\)
TH2 : Thay x = 2 vào biểu thức P ta được : \(P=\dfrac{2+\sqrt{2}+1}{2}=\dfrac{3+\sqrt{2}}{2}\)
Giải hộ mình với!
5 tháng 11 2021
\(a,=\left[\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}-\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right]\left(\sqrt{7}+\sqrt{5}\right)\\ =\left(-\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}+\sqrt{5}\right)=5-7=-2\)
31 tháng 12 2023
a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)EB tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
=>BF\(\perp\)FC tại F
=>BF\(\perp\)AC tại F
Xét ΔABC có
BF,CE là các đường cao
BF cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp đường tròn đường kính AH
tâm K là trung điểm của AH
b:
Ta có: OE=OC
=>ΔOEC cân tại O
=>\(\widehat{OEC}=\widehat{OCE}\)
Ta có: ΔKHE cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
\(\widehat{KEO}=\widehat{KEC}+\widehat{OEC}\)
\(=\widehat{OCE}+\widehat{KHE}\)
\(=\widehat{ECB}+\widehat{DHC}=90^0\)
=>KE là tiếp tuyến của (O)
Xét ΔKEO và ΔKFO có
KE=KF
EO=FO
KO chung
Do đó: ΔKEO=ΔKFO
=>\(\widehat{KEO}=\widehat{KFO}=90^0\)
Ta có: \(\widehat{KEO}=\widehat{KFO}=\widehat{KDO}=90^0\)
=>K,E,O,F,D cùng thuộc đường tròn đường kính KO(ĐPCM)
13 tháng 6 2021
*Chữ xấu+Chụp mờ+Viết tắt nhiều đáng lẽ là mình không giải đâu nhưng.....
Bạn tham khảo 2 ý a,b trước
a)Vì CM,CN là 2 tt của (O,R)
`=>hat{CMO}=hat{CNO}=90^o`
Vì `hat{CMO}=90^o`
`=>M` thuộc đường tròn đường kính OC(1)
Vì `hat{CNO}=90^o`
`=>N` thuộc đường tròn đường kính OC(2)
Xét (O,R) có:
`H` là trung điểm AB
`=>OH bot AB`
`=>hat{CHO}=90^o`
`=>H` thuộc đường tròn đường kính OC(3)
`(1)(2)(3)=>C,M,H,O,N` cùng thuộc đường tròn đường kính OC tức là cùng nằm trên 1 đường tròn
Tam giác CMN là tam giác nội tiếp.
`=>` tâm đường tròn ngoại tiếp `Delta CMN` nằm ở trung điểm OC
Mà `IM=IN`
`=>I` cách đều các cạnh tam giác CMN
`b)` Vì CM=CN(do CM,CN là 2 tt cắt tại C)6
`OM=ON=R`
`=>CO` là trung trực MN
`=>hat{CQN}=90^o`
Vì C,M,H,N cùng thuộc 1 đường tròn
`=>` tg CMHN nt
`=>hat{CHM}=hat{CNM}`
Mà `hat{CNM}+hat{QCN}=90^o(cmt)`
`hat{CON}+hat{QCN}=90^o`
`=>hat{CNM}=hat{CON}`
Mà `hat{CHM}=hat{CNM}`
`=>hat{CON}=hat{CHM}`
Vì C,H,O,N cùng thuộc 1 đường tròn
`=>` tg CHON nt
`=>hat{CHN}=hat{CON}`
`=>hat{CHM}=hat{CHN}`
`=>HC` là pg `hat{MHN}`
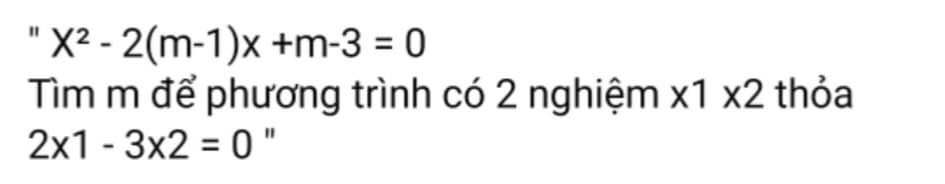
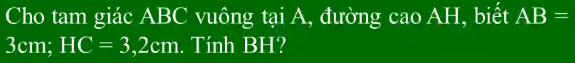
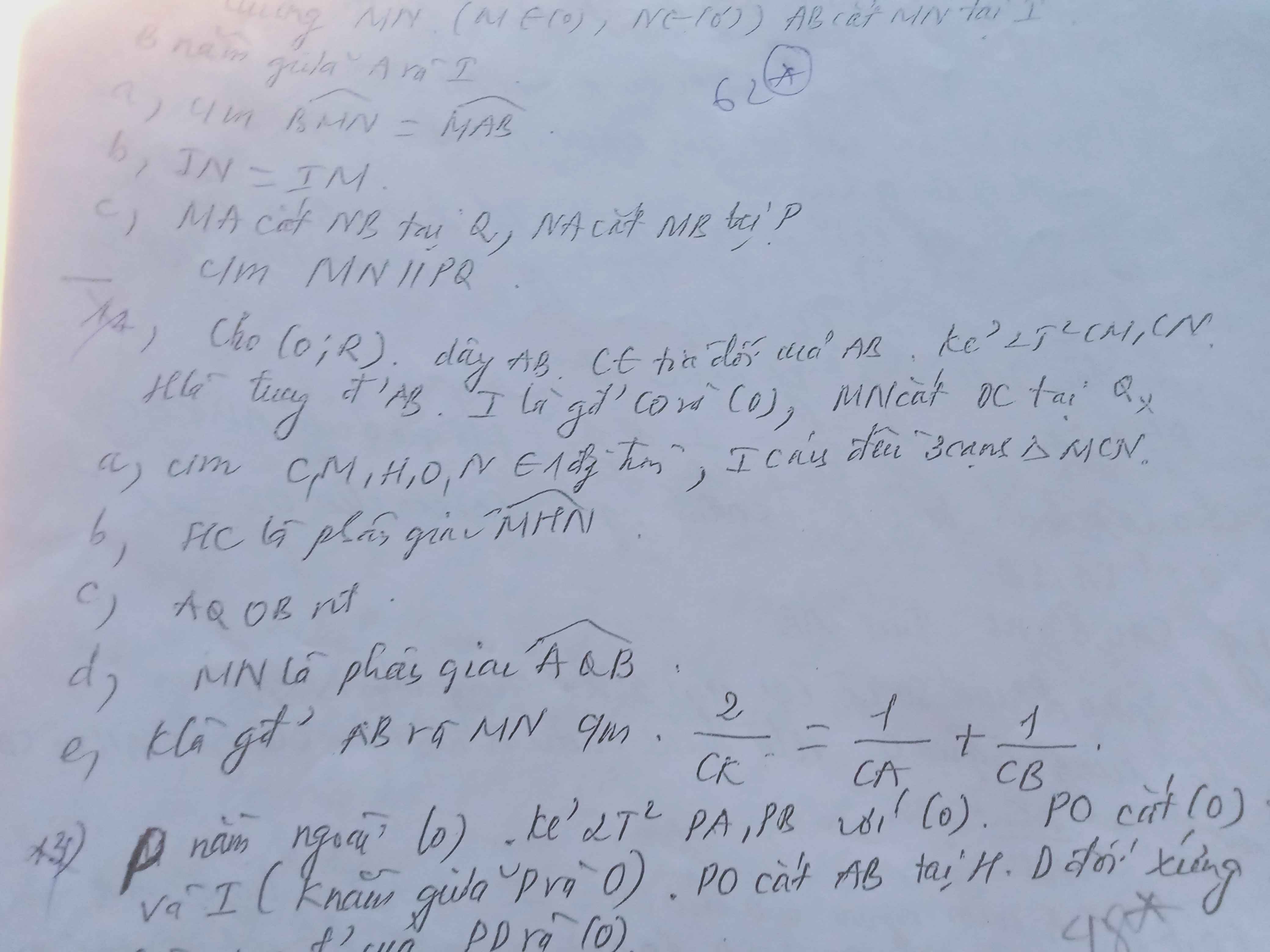
\(M=\sqrt{18}-\sqrt{8}\)
\(\Rightarrow M^2=18+8-2\sqrt{18.8}=2\)
\(\Rightarrow M=\sqrt{2}\)( vì M >0 )
+) \(N=\frac{5+\sqrt{5}}{\sqrt{5}+1}-\sqrt{6-2\sqrt{5}}\)
\(=\frac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}-\sqrt{6-2\sqrt{5}}\)
\(=\sqrt{5}-\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=\sqrt{5}-\sqrt{5}+1=1\)
M>N