Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



- Công của lực được tính theo công thức: \(A=F.s.cosα\)
- Trong đó:
+) A : công của lực (J)
+) F: lực (N)
+) α : góc tạo bởi đường đi của vật và lực F.
Mà: vật chuyển dời theo phương vuông góc.
⇒ \(A=F.s.cosα=F.s.cos90^o =F.s.0=0(J)\)
Vậy vật chuyển dời theo phương vuông góc với phương của lực thì công của lực đó bằng 0.


Câu 1: Khi đi trên sàn đá hoa mới lau dễ bị ngã vì lực ma sát nghỉ giữa sàn vơi chân người rất nhỏ => Ma sát trong hiện tượng này có ích.
Câu 2: *Mình nghĩ đề phải đi trên cùng 1 đường và bắt đầu cùng 1 thời gian thì mới làm được*
a) Người thứ 2 đi nhanh hơn do Vận tốc của người thứ 2 nhanh hơn Vận tốc của người thứ nhất.
b)

Gọi A là điểm xuất phát của người 2, B là điểm xuất phát của người thứ 1. C là điểm gặp của 2 người.
\(V_1;V_2\) lần lượt vận tốc của người thứ nhất và người thứ 2.
t là thời gian đi của 2 xe.
Ta có: \(S_{AC}-S_{AB}=17\Rightarrow V_2.t-V_1t=17\Rightarrow60t-40t=20t=17\Rightarrow t=0,86\left(h\right)\)
Câu 3:

Diễn tả bằng lời:
\(\overrightarrow{P}\) là trọng lương của vật đặt tại tâm của vật, phương thẳng đứng chiều từ trên xuống.
\(\overrightarrow{F}\) được đặt tại tâm của vật, phương thẳng đứng chiều từ dưới lên.
Câu 4: Tóm tắt
\(t_1=\frac{1}{3}t\)
\(V_1=12m\)/\(s\)
\(t_2=\frac{2}{3}t\)
\(V_2=9m\)/\(s\)
_________
\(V_{TB}\)=?
Gỉai
Gọi \(S_1;S_2\) lần lượt là quãng đường đi với vận tốc 12km/h; 9 km/h
Ta có công thức sau: \(V_{TB}=\frac{S_1+S_2}{t_1+t_1}\)
Trong đó: \(S_1=V_1.t_1=12.\frac{1}{3}t=4t;S_2=V_2.t_2=9.\frac{2}{3}t=6t\)
\(\Rightarrow V_{TB}=\frac{4t+6t}{t}=10\) ( m/s)

Có phải là trọng lượng riêng của nước biển là 10300 \(N\)/\(m^3\)
và trọng lượng riêng của xăng là \(7000N\)/\(m^3\)
Với lại là tìm độ cao của cột xăng chứ tính cột nước thì bao nhiêu chả được.
Tóm tắt.
\(h'=20cm\)
\(d_1=10300N\)/\(m^3\)
\(d_2=7000N\)/\(m^3\)
_____________
\(h=?\)
Giải

Xét A là điểm nằm ở đáy cột xăng và B là điểm nằm cùng một mặt phẳng nằm ngang với điểm A (Trong lòng cột nước biển)
Ta có: \(p_A=p_B\) và \(h_1+h'=h\Rightarrow h_1+20=h\)
\(\Rightarrow d_1.h=d_2.h_1\Rightarrow d_1.\left(h_1+h'\right)=d_2.h_1\Rightarrow7000\left(h_1+20\right)=10300.h_1\)
\(\Rightarrow7000h_1+140000=10300h_1\Rightarrow140000=3300h_1\Rightarrow h_1\approx42\left(cm\right)\)

Gọi quãng đường đầu là AC, quãng đường sau là CB (thỏa mãn AC + CB = AB).
Ta có công thức tính \(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}\) (áp dụng cho bài này).
Suy ra \(\dfrac{S_{AC}+S_{CB}}{t_{AC}+t_{CB}}=\dfrac{S_{AC}+S_{CB}}{\dfrac{S_{AC}}{v_{AC}}+\dfrac{S_{CB}}{v_{CB}}}\) , mà \(S_{AC}=S_{CB}\)
\(\Rightarrow\dfrac{1}{\dfrac{1}{\dfrac{2}{20}}+\dfrac{1}{\dfrac{2}{30}}}=24\)(km/h).
Vậy vận tốc trung bình là 24 km/h.
Bài làm
Gọi V1, V2 lần lượt là vận tốc của người này trên nửa quãng đường đầu và nửa quãng đường còn lại.
Gọi t1, t2 lần lượt là thời gian của người này trên nửa quãng đường đầu và nửa quãng đường còn lại.
Gọi S1, S2 lần lượt là nửa quãng đường đầu và nửa quãng đường còn lại.
Vận tốc trung bình của người đó = \(\dfrac{S1+S2}{t1+t2}\)
Vì hai quãng đường S1 và S2 bằng nhau nên \(\dfrac{2S}{t1+t2}\)
Theo công thức V=\(\dfrac{S}{t}\) suy ra t=\(\dfrac{S}{V}\) ta có \(\dfrac{2S}{\dfrac{S}{V1}+\dfrac{S}{V2}}\)
Thay V1 = 20; V2 = 30 ta có \(\dfrac{2S}{\dfrac{S}{20}+\dfrac{S}{30}}\)
Bỏ S ra ngoài ta có \(\dfrac{2S}{S\left(\dfrac{1}{20}+\dfrac{1}{30}\right)}\)
Bỏ S ở cả tử và mẫu ta có \(\dfrac{2}{\dfrac{1}{20}+\dfrac{1}{30}}\)
Kết quả cuối cùng ta được 24(km/h)
Vậy vận tốc trung bình của người này trên cả đoạn đường AB là 24 km/h.



Câu 1 : C
Câu 2 : D
Câu 3 : B
Câu 4 : C
Câu 5 : B
Câu 6 : A
Phần 2
1 Nhiệt lượng là phần nhiệt năng , mà vật nhận được thêm hoặc mất bớt đi , trong khi truyền nhiệt
2 Nhiệt lượng truyền từ vật có nhiệt độ cao hơn , sang vật có nhiệt độ thấp hơn
Sự truyền nhiệt xảy ra cho tới khi nhiệt độ của hai vật cân bằng nhau thì ngừng lại
Nhiệt lượng do vật này tỏa ra bằng nhiệt lượng do vật kia thu vào
Chúc bạn học tốt
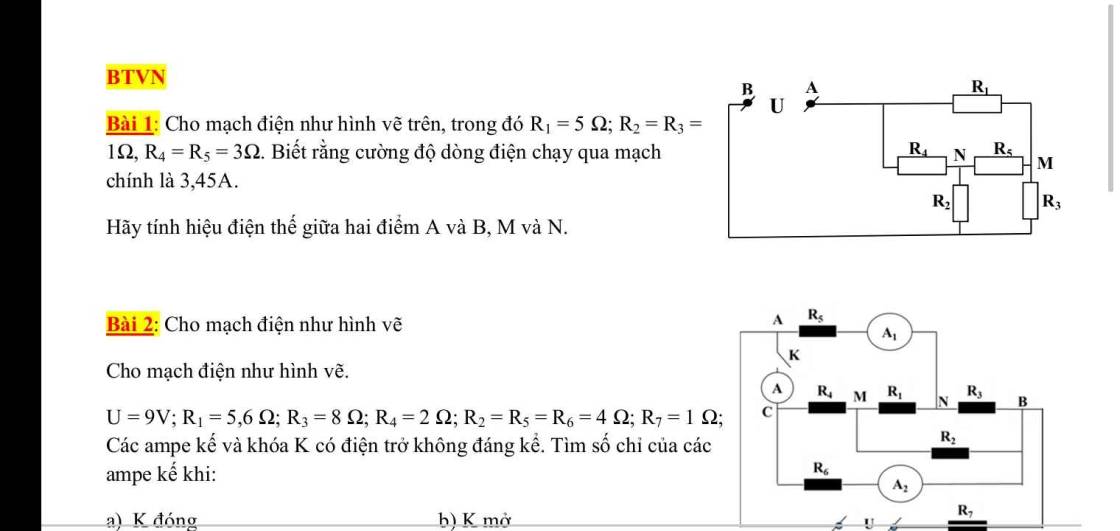



 ai giải hộ em bài này với
ai giải hộ em bài này với Giải hộ em bài 4 với ạ T_T
Giải hộ em bài 4 với ạ T_T