
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,x^3y^2-xy^2=xy^2\left(x^2-1\right)=xy^2\left(x-1\right)\left(x+1\right)\\ b,2x^3y^2+4x^2y^2+2xy^2=2xy^2\left(x^2+2x+1\right)=2xy^2\left(x+1\right)^2\\ c,3x^3y-12x^2y+12xy=2xy\left(x^2-4x+4\right)=2xy\left(x-2\right)^2\\ d,6x^3y+12x^2y^2+6xy^3=6xy\left(x^2+2xy+y^2\right)=6xy\left(x+y\right)^2\\ e,x^2\left(x-y\right)+y^2\left(y-x\right)=\left(x^2-y^2\right)\left(x-y\right)=\left(x-y\right)^2\left(x+y\right)\\ f,9x^2\left(x-2\right)-4y^2\left(x-2\right)=\left(9x^2-4y^2\right)\left(x-2\right)=\left(3x-2y\right)\left(3x+2y\right)\left(x-2\right)\)
Tick plz
a: \(x^3y^2-xy^2=xy^2\left(x^2-1\right)=xy^2\left(x-1\right)\left(x+1\right)\)
b: \(2x^3y^2+4x^2y^2+2xy^2=2xy^2\left(x^2+2x+1\right)=2xy^2\cdot\left(x+1\right)^2\)
c: \(3x^3y-12x^2y+12xy=3xy\left(x^2-4x+4\right)=3xy\cdot\left(x-2\right)^2\)
d: \(6x^3y+12x^2y^2+6xy^3=6xy\left(x^2+2xy+y^2\right)=6xy\cdot\left(x+y\right)^2\)
e: \(x^2\left(x-y\right)+y^2\left(y-x\right)=\left(x-y\right)^2\cdot\left(x+y\right)\)
f: \(9x^2\left(x-2\right)-4y^2\left(x-2\right)=\left(x-2\right)\left(3x-2y\right)\left(3x+2y\right)\)

`(x+1)(x+3)=2x^2-2`
`<=>x^2+x+3x+3=2x^2-2`
`<=>x^2-4x-5=0`
`<=>x^2-5x+x-5=0`
`<=>x(x-5)+(x-5)=0`
`<=>(x-5)(x+1)=0`
`<=>` $\left[ \begin{array}{l}x=5\\x=-1\end{array} \right.$
Vậy `S={5,-1}`
Ta có: \(\left(x+1\right)\left(x+3\right)=2x^2-2\)
\(\Leftrightarrow\left(x+1\right)\left(x+3\right)-2x^2+2=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+3\right)-2\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+3\right)-2\left(x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[x+3-2\left(x-1\right)\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+3-2x+2\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(5-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\5-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=5\end{matrix}\right.\)
Vậy: S={-3;5}

a: Ta có: \(x\left(2-3x\right)+\left(3x^3-x^2\right):x\)
\(=2x-3x^2+3x^2-x\)
=x
b: Ta có: \(2x\left(x-3y\right)-\left(8x^3y-12x^2y^2\right):2xy\)
\(=2x^2-6xy-4x^2+6xy\)
\(=-2x^2\)

Mình sẽ làm theo đề bài của mình nếu đúng thì ... nha
Biến đổi vế phải ta có :
( x + y) [ ( x - y)^2 + xy ] = ( x + y)( x^2 - 2xy + y^2 + xy)
= ( x+ y)( x^2 - xy+ y^2)
= x^3 + y^3
VẬy VT = VP đẳng thức được CM

\(\left(x-2\right)\left(x-3\right)=\left(x-2\right)\left(x+1\right)\)
\(\Leftrightarrow x^2-5x+6=x^2-x-2\)
\(\Leftrightarrow-4x+8=0\)
\(\Leftrightarrow x=2\)
Vậy ...

\(a,3\left(x^2-7\right)-x\left(3x+5\right)=3x^2-21-3x^2-5x=-5x-21\\ b,\left(12x^2y^2-6xy\right):3xy+2y=3xy\left(4xy-2\right):3xy+2y=4xy-2+2y\)
\(c,\dfrac{4}{x+1}+\dfrac{8}{\left(x-1\right)\left(x+1\right)}=\dfrac{4\left(x-1\right)+8}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x-4+8}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}\)

\(C=x^2-xy+x-y^2-y+xy\)
\(C=x^2-y^2+x-y=\left(x-y\right)\left(x+y+1\right)\)
Học tốt :))
Rút gọn ạ ? -.-
C = x( x - y + 1 ) - y( y + 1 - x )
= x2 - xy + x - y2 - y + xy
= x2 - y2 + x - y

các bạn giải hộ mình với :
a,X3 - 30X2 - 31X + 1 với X = 31
b,X5 - 15X4 + 16X3 - 29X2 + 13X với X = 14


Lời giải:
ĐKXĐ: $x\neq \pm 4$
PT $\Leftrightarrow \frac{8(x-4)+8(x+4)}{x^2-16}=\frac{25}{3}$
$\Leftrightarrow \frac{16x}{x^2-16}=\frac{25}{3}$
$\Rightarrow 48x=25x^2-400$
$\Leftrightarrow 25x^2-48x-400=0$
$\Leftrightarrow (5x-\frac{24}{5})^2=\frac{10576}{25}$
$\Rightarrow x=\frac{24\pm 4\sqrt{661}}{25}$ (đều thỏa mãn)
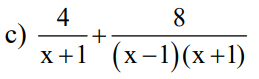
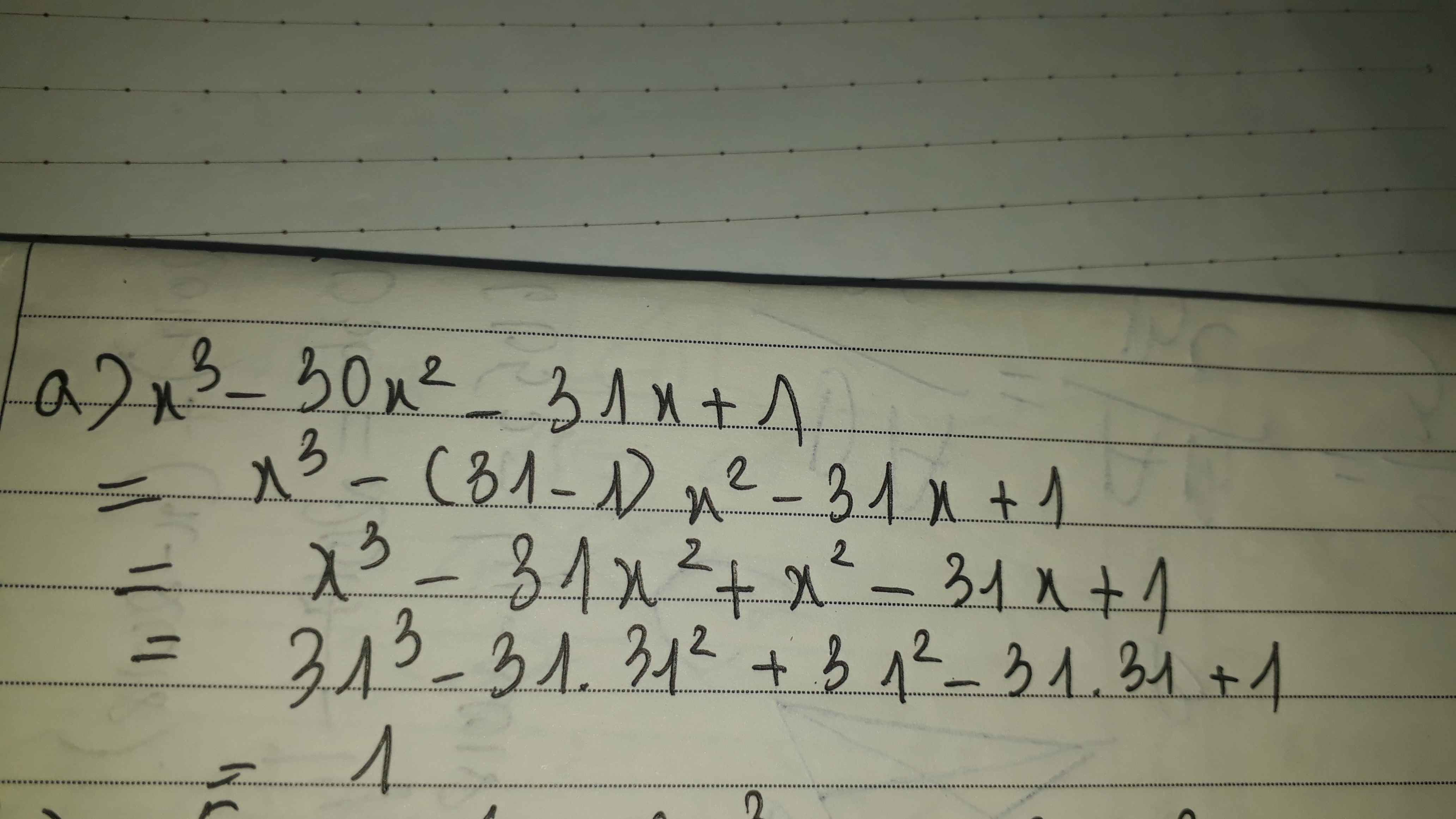

\(4xy^2\cdot x-\left(-12x^2y^2\right)\)
\(=4x^2y^2+12x^2y^2\)
\(=16x^2y^2\)